


Next: The Phugoid model
Up: Using Maple
Previous: A nod toward statistics
In this chapter, we will explore some aspects of mathematical model of
glider flight. This model is called Lanchester's
phugoid theory3.1, developed by Frederick Lanchester [Lan] at
beginning of the twentieth century.
While this model has its drawbacks, it still is used today to
explain oscillations and stalls in airplane flight.
Since this model, like many models, is a set of differential equations, we
will need some results which are typically covered in a course on
differential equations. We will cover the relevant material briefly here,
but readers needing a more in-depth treatment are encouraged to look in a
text on ordinary differential equations, such as
[BDH], [HW], or [EP].
Of these, the approach in [BDH] is perhaps closest to
the one presented here.
Footnotes
- ... theory3.1
- Folklore has it that this name was
chosen by Lanchester because he wanted a classically-based name for his
new theory of oscillations occuring during flight. Since the Greek root
phug (
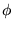
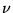
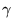
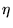 , pronounced ``fyoog'') as well as the
Latin root fug- both correspond to the English word ``flight'',
he decided on the name ``phugoid''. Unfortunately, in both Greek and
Latin, this means ``flight'' as in ``run away'' instead of what birds
and airplanes do-- the same root gives rise to the words ``fugitive'' and
``centrifuge''. The Latin for flight in appropriate sense is
volatus; the Greek word is potê (
, pronounced ``fyoog'') as well as the
Latin root fug- both correspond to the English word ``flight'',
he decided on the name ``phugoid''. Unfortunately, in both Greek and
Latin, this means ``flight'' as in ``run away'' instead of what birds
and airplanes do-- the same root gives rise to the words ``fugitive'' and
``centrifuge''. The Latin for flight in appropriate sense is
volatus; the Greek word is potê (
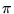 o
o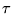
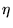 ).
).
Subsections



Next: The Phugoid model
Up: Using Maple
Previous: A nod toward statistics
Translated from LaTeX by Scott Sutherland
2002-08-29