The Phugoid model

The Phugoid model is a system of two nonlinear differential equations in a frame of reference relative to the plane. Let v(t) be the speed the plane is moving forward at time t, and $\theta$(t) be the angle the nose makes with the horizontal. As is common, we will suppress the functional notation and just write v when we mean v(t), but it is important to remember that v and $\theta$ are functions of time.

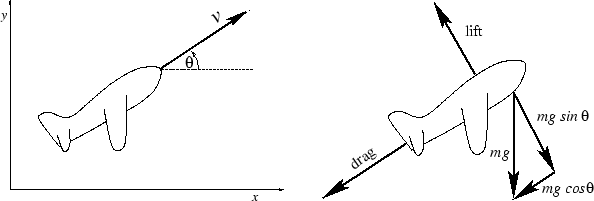
If we apply Newton's second law of motion (force = mass × acceleration) and examine the major forces acting on the plane, we see easily the force acting in the forward direction of the plane is

m$${\frac{dv}{dt}}$$ = - mg sin$$\theta$$ - drag.

This matches with our intuition: When $\theta$ is negative, the nose is pointing down and the plane will accelerate due to gravity. When $\theta$ > 0, the plane must fight against gravity.

In the normal direction, we have centripetal force, which is often expressed as mv²/r, where r is the instantaneous radius of curvature. After noticing that that ${\frac{d\theta}{dt}}$ = v/r, this can be expressed as v${\frac{d\theta}{dt}}$, giving

mv$${\frac{d\theta}{dt}}$$ = - mg cos$$\theta$$ + lift.

Experiments show that both drag and lift are proportional to v², and we can choose our units to absorb most of the constants. Thus, the equations simplify to the system

$${\frac{dv}{dt}}$$ = - sin$$\theta$$ - Rv²                $${\frac{d\theta}{dt}}$$ = $${\frac{v^2 - \cos\theta}{v}}$$

which is what we will use henceforth. Note that we must always have v > 0.

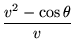
It is also common to use the notation $\dot{v}$ for ${\frac{dv}{dt}}$ and $\dot{\theta}$ for ${\frac{d\theta}{dt}}$. We will use these notations interchangeably.