Seeing the flight path

In §2, we exhibited a number of solutions to the phugoid model with various initial conditions and values for the drag, as plots of the parametric curves [$\theta$(t), v(t)]. From these, we could deduce an approximate path of the glider through space via reasoning like ``$\theta$(t) is monotonically increasing, so the glider must be doing loop-the-loops''. We will now discuss how to solve for the position [x(t), y(t)] directly.

First, notice that if we know the value of v and $\theta$ at some time t, we also have ${\frac{dx}{dt}}$ and ${\frac{dy}{dt}}$ at that t, since

$${\frac{dx}{dt}}$$ = v cos$$\theta$$        and        $${\frac{dy}{dt}}$$ = v sin$$\theta$$.

So, one way to find x(t) and y(t) would be to solve the original ODE (numerically) for $\theta$(t) and v(t), obtain a new differential equation, and then solve that numerically for x(t) and y(t).

Aside from the fact that there is an easier way, there is a serious practical problem with this approach. When we get a numerical solution [$\theta$(t), v(t)], this is a collection of points ($\theta_{0}^{}$, v₀, t₀),($\theta_{1}^{}$, v₁, t₁), ... ,($\theta_{n}^{}$, v_n, t_n) along a curve. This means we only know the vector field for (x, y) at those points. It is highly unlikely that these will be the points we need to use Runge-Kutta. We could use these to approximate our (x, y)-solution using Euler's method, although even then we would have to program it ourselves rather than use Maple's built-in method.

If you think for just a moment, you should realize that there is no reason we must find $\theta$(t) and v(t) before attempting to find x(t) and y(t). Instead, we can augment the original system, adding in the new equations for $\dot{x}$ and $\dot{y}$. Then, we can use numerical methods to solve for [$\theta$(t), v(t), x(t), y(t)] all in one step. The methods we discussed in §4.2 apply equally well to vector fields in any number of variables.

Consequently, we rewrite our phugoid system as

$${\frac{d\theta}{dt}}$$ = $${\frac{v^2 - \cos\theta}{v}}$$        $${\frac{dv}{dt}}$$ = - sin$$\theta$$ - Rv²        $${\frac{dx}{dt}}$$ = v cos$$\theta$$        $${\frac{dy}{dt}}$$ = v sin$$\theta$$.

Using this system, we need to specify our initial conditions as ($\theta_{0}^{}$, v₀, x₀, y₀), and each solution is a curve in $\R^{4}_{}$ parameterized by time. We can take a projection of this curve to get our solutions in $\theta$-v or x-y coordinates.

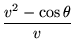
Asking Maple to solve this new system is almost the same as before, but we must specify the additional variables and use the scene option to DEplot to tell Maple which projection we want to see. Note that we reset R to ensure that it appears in the equations as an arbitrary constant, rather than with any previously assigned value.

> 
  R:=`R`:
  xphug :=[ diff(theta(t),t) =  (v(t)^2 - cos(theta(t)))/v(t),
            diff(v(t),t)     =  -sin(theta(t)) - R*v(t)^2 ,
            diff(x(t),t)     =  v(t)*cos(theta(t)),
            diff(y(t),t)     =  v(t)*sin(theta(t))];

Now we ask Maple to plot two solution curves in both $\theta$, v coordinates and x, y. One is started with an initial angle of $\theta$ = 0 and velocity v = 1.5 at a height y(0) = 1; the other starts with $\theta$ = 0, v = 2.5, and initial height y = 2. We also use display with an array to show the two scenes side by side.

> 
  R:=0;
  plots[display](array([
   DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[theta,v]),
  

  DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[x,y]),
   ])));

R : = 0;

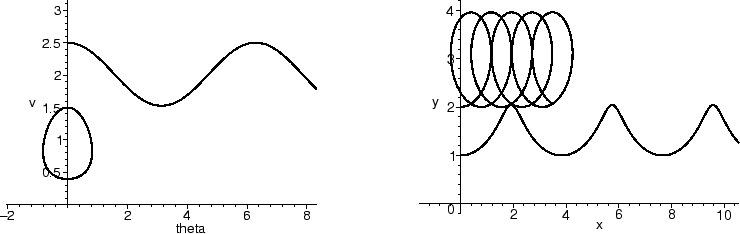
If we change the value of R to 0.2 and repeat the command, we can see how things change when there is friction. Notice how spiraling towards the fixed point in the $\theta$-v coordinates corresponds to a plane which is diving with an oscillatory motion.

> 
  R:=0.2;
  plots[display](array([
   DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[theta,v]),
  

  DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[x,y]),
   ])));

R : = 0.2;

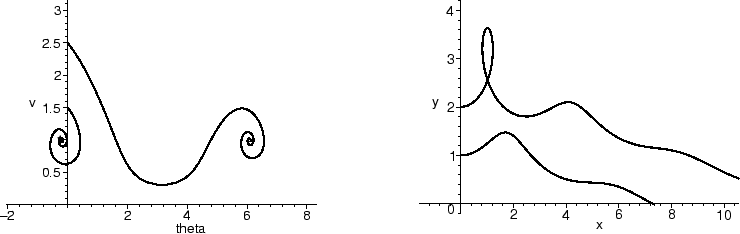
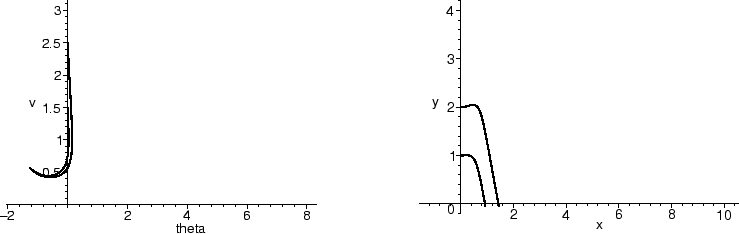
Finally, we redo the pictures with a large amount of friction (R = 3). Note how the glider acts more like a rock than a glider, and there is no oscillation at all.

> 
  R:=3;
  plots[display](array([
   DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[theta,v]),
  

  DEplot(xphug, [theta,v,x,y], t=0..15, 
    [[theta(0)=0,v(0)=1.5,x(0)=0,y(0)=1],[theta(0)=0,v(0)=2.5,x(0)=0,y(0)=2]],
    theta=-Pi..5*Pi/2, v=0.1..3, x=-1..10, y=0..4,
    linecolor=black, stepsize=0.1, scene=[x,y]),
   ])));

R : = 3;