So far, the cases we've looked at seem to have a number of common features.
Each has has a solution with ![]() (t) and v(t) constant; there are
solutions which immediately tend toward the constant solution (or oscillate
around it), and solutions which do some number of loops first (for R = 3, we
didn't demonstrate this- if the inital angle is 0, a solution needs an
initial velocity larger than 86.3 before it will do a loop).
How do the possible solutions depend on the value of R? For example,
the behavior of solutions for R = 0.1 and R = 0.2 are quite similar, but are
dramatically different from R = 0 and R = 3.
(t) and v(t) constant; there are
solutions which immediately tend toward the constant solution (or oscillate
around it), and solutions which do some number of loops first (for R = 3, we
didn't demonstrate this- if the inital angle is 0, a solution needs an
initial velocity larger than 86.3 before it will do a loop).
How do the possible solutions depend on the value of R? For example,
the behavior of solutions for R = 0.1 and R = 0.2 are quite similar, but are
dramatically different from R = 0 and R = 3.
One way we can get a better handle on exactly how the behavior of the
solutions depends on R is to examine what happens to solutions near the
constant solution. If we look in the ![]() -v plane, this solution
corresponds to a single point, which is often referred to as a ``fixed
point''. We explicitly found the fixed point
{
-v plane, this solution
corresponds to a single point, which is often referred to as a ``fixed
point''. We explicitly found the fixed point
{![]() (t) = 0, v(t) = 1}
solution for R = 0 in §2 by noticing that
whenever
(t) = 0, v(t) = 1}
solution for R = 0 in §2 by noticing that
whenever
![]() = 0 and
= 0 and ![]() = 0, we must have a constant solution
(and vice-versa). Using
= 0, we must have a constant solution
(and vice-versa). Using
![]() solve, we can get maple to tell us the
where the fixed point is for arbitrary values of R. We use convert
to insist that maple represent the result as a radical, instead of using the
RootOf notation.
solve, we can get maple to tell us the
where the fixed point is for arbitrary values of R. We use convert
to insist that maple represent the result as a radical, instead of using the
RootOf notation.
>
R:='R':
FixPoint:=convert(
solve((v^2-cos(theta))/v=0,-sin(theta)-R*v^2=0, theta,v),
radical);
![]()
So, we see that there is a fixed point for all values of R (since 1 + R2 is always positive, the radical always takes real values). For R > 0,
What can we say about behaviour of solutions near this fixed solution?
In order to answer this, notice that we can apply Taylor's theorem to the right-hand side of our system of differential equations. That is, think of our differential equation as being in the vector form
First, we give a brief refresher about linear 2×2 systems of
equations. The reader is refered to the texts in the references for more
comprehensive treatment of this topic.
Linear differential equations (with constant coefficients) are the simplest
ones to solve and understand. Such equations have the form
![]() = AX,
where A is an n×n matrix and X is an n-vector. We'll
be content with n = 2.
= AX,
where A is an n×n matrix and X is an n-vector. We'll
be content with n = 2.
First, notice that X = 0 is always a fixed point for this system, and it is the only one. Secondly, if X1(t) and X2(t) are solutions to the system, then so is X1(t) + X2(t). This property is called superposition and will be very useful.
Let's look at the simplest case for the 2×2 system:
A = ![]()
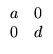
![]() , that is,
, that is,
| = | ax | ||
| = | dy |
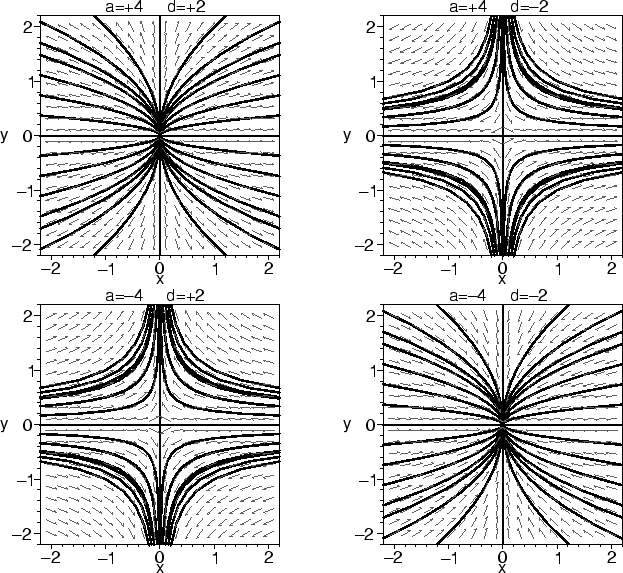
A large number of linear systems behave very similarly to the cases above, except the straight-line solutions may not lie exactly along the coordinate axes.
Suppose there is a solution of
To find the eigenvalues, we need to solve
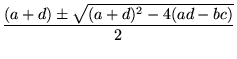 .
.
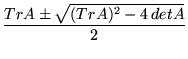 .
.
For linear systems, the eigenvalues determine the ultimate fate of solutions
to the ODE. From the above, it should be clear that there are always two
eigenvalues for a 2×2 matrix (although sometimes there might be a
double eigenvalue, when
(TrA)2 - 4 detA = 0).
Let's call them ![]() and
and ![]() .
.
We've already seen prototypical examples where the eigenvalues are real, nonzero, and distinct. But what if the eigenvalues are complex conjugate (which happens when (TrA)2 < 4 detA)? In this case, there is no straight line solution in the reals. Instead, solutions turn around the origin. If the real part of the eigenvalues is positive, solutions spiral away from the origin, and if it is negative, they spiral towards it. If the eigenvalues are purely imaginary, the solutions neither move in nor out; rather, they circle around the origin.
We can summarize this in the table below. We are skipping over dealing with
the degenerate cases, when
![]() =
= ![]() and when one of the
eigenvalues is zero.
and when one of the
eigenvalues is zero.
|
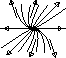 |
|
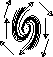 |
|||
|
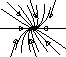 |
|
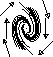 |
|||
|
 |
|
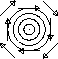 |
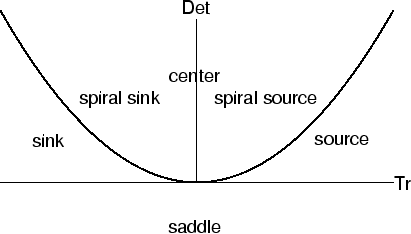
Finally, we remark that there is a convenient way to organize this information into a single diagram. Since the eigenvalues of A can be written as
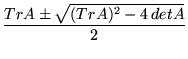 ,
,
We now return to our nonlinear system, and look at the linearization near the fixed point. As we saw earlier in this section, for every value of R the Phugoid model
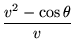
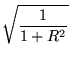
![$\displaystyle \sqrt[4]{\frac{1}{1 + R^2}}$](img351.gif) .
.
> with(linalg): R:='R': J:=jacobian( [(v^2-cos(theta))/v, -sin(theta)-R*v^2], [theta, v]);
![\begin{maplelatex}
\begin{displaymath}
J := \left[
{\begin{array}{cc}
{\display...
...s}(\theta ) & - 2 R v
\end{array}}
\right]
\end{displaymath}\end{maplelatex}](img352.gif)
Once we know the trace and determinant of the Jacobian matrix at the fixed point, we can use that information to determine how its type (sink, source, saddle, etc.) depends on R. Rather than solve for the eigenvalues directly, we will compute the trace and determinant, which have a simpler form in this case.
First, let's find the fixed point again, issuing the same command we did earlier. Then, we'll substitute that into the result of trace and det to calculate the trace and determinant at the fixed point.
>
FixPoint:=convert(
solve((v^2-cos(theta))/v=0,-sin(theta)-R*v^2=0, theta,v),
radical);
![]()
>
trfix := simplify(subs(FixPoint, trace(J)));
detfix:= simplify(subs(FixPoint, det(J)));
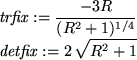
So, we see that for all real values of R, the determinant is positive
(meaning saddles are impossible). Furthermore, for R > 0, the trace is
negative, so the fixed point is always a sink. (When R = 0, the trace is
zero, which means it is possible for this fixed point to be a
center.3.5)
From the plots we made earlier, we expect that for small values of R, we
will have a spiral sink, but it will probably not spiral for sufficiently
large values of R. We can check this by solving for the point where
Tr(J)2 = 4 det(J), which happens when
R = 2![]() .
.
>
solve( (trfix)^2 = 4*detfix, R);
![]()