Existence of Solutions

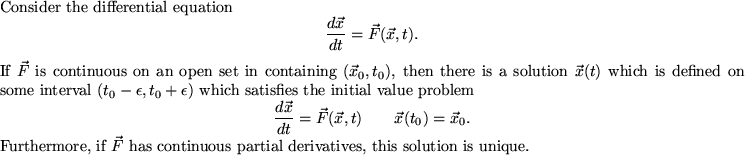
We've been acting as though just by specifying an initial condition, there must be a solution, and it must be unique (that is, the only one corresponding to that initial condition). And, in fact, this is typically true for any ``nice'' differential equation. But which differential equations are ``nice'' enough?

We won't prove the theorem here, but we will state it. The reader is encouraged to look up the proof in any differential equations text, such as [BDH] or [HW].

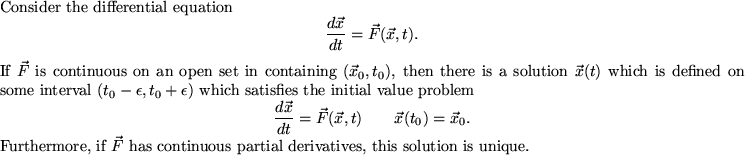
In fact, the hypothesis can be weakened a little bit and still preserve the uniqueness. As long as $\vec{F}$ is at least Lipshitz in $\vec{x}$, the solution will be unique. A function $\vec{F}$ if called Lipschitz if there is some K so that

|$$\vec{F}$$($$\vec{x}_{1}^{}$$, t) - $$\vec{F}$$($$\vec{x}_{2}^{}$$, t)| < K|$$\vec{x}_{1}^{}$$ - $$\vec{x}_{2}^{}$$|

for all t, $\vec{x}_{1}^{}$, and $\vec{x}_{2}^{}$. This condition says, roughly, that $\vec{F}$ doesn't spread out too quickly. All functions with continuous partials are automatically Lipshitz.

This means that for us, as long as we stay away from the place where our differential equation isn't defined (i.e. ensure that v > 0), we can be assured that there is a solution through every point, and that solution is unique. Notice that since our equations are autonomous (the right-hand side has no explict dependence on t), uniqueness of solutions means that solutions cannot cross in the ($\theta$, v)-plane.