Improved Caesar-like ciphers

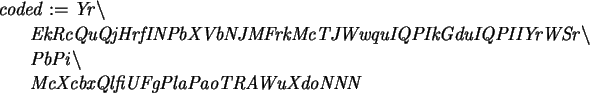
Certainly the Caesar cipher offers no cryptographic security at all: if you know the alphabet the message was encoded in, you need only guess one character to crack the code. Even if you don't know the alphabet, guessing the correspondence is not very hard with a little patience.

In this section, we will discuss a few approaches to improving the security, while retaining the basic idea of character shifting.

The Vignère cipher

One way to make a Caesar cipher a bit harder to break is to use different shifts at different positions in the message. For example, we could shift the first character by 25, the second by 14, the third by 17, and the fourth by 10. Then we repeat the pattern, shifting the fifth character by 25, the sixth by 14, and so on, until we run out of characters in the plaintext. Such a scheme is called a Vignère cipher ^3.8, which was first used around 1600, and was popularly believed to be unbreakable. ^3.9

In our example, the key consists of the four shifts [25, 14, 17, 10], which are the numerical equivalents of the string ``ZORK'' in a 26-letter alphabet consisting of the letters A-Z. It is common practice to think of our key as plaintext letters, rather than their numerical equivalents, but either will do. We can encode the string ``CRYPTOGRAPH'' as

C	R	Y	P	T	O	G	R	A	P	H
+25	+14	+17	+10	+25	+14	+17	+10	+25	+14	+17
B	F	P	Z	S	C	X	B	Z	D	Y

Note that in the above, the letter ``R'' in the plaintext encodes to both ``F'' and ``B'' in the crypttext, depending on its position. Similarly, the two ``Z''s in the crypttext come from different plain characters.

But, still, this is not very hard to crack. If we know that the key is of a certain length, say 4, and our plaintext is sufficiently long, then we can perform frequency analysis on every fourth letter. Even if we don't know the length, it is not too hard to write a computer program to try all the lengths less than, say, 10, and pick the one that looks best.

 

> Alphabet := `ABCDEFGHIJKLMNOPQRSTUVWXYZ
  abcdefghijklmnopqrstuvwxyz., `:
    
  Vignere:= proc(plaintext, key)
    local textnum,codenum,i,p,offsets,keylen;
    global Alphabet;
    
    p       := length(Alphabet);
    offsets := ToNum(key);
    keylen  := length(key);
    textnum := ToNum(plaintext);
    codenum := [seq(
                    modp(textnum[i] + offsets[modp(i-1,keylen)+1], 
                         p),
                    i=1..length(plaintext)) ];  
    FromNum(codenum);
  end:

> coded:=Vignere(test,`Prufrock`);

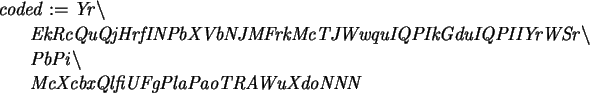
We can make the decoding function from the original (let's call it unVignere) by changing exactly one + sign to a -.^3.10 We omit the change here so perhaps you will figure it out for yourself. But we will test it, to show you that it does work.

> unVignere(code,`Prufrock`);

One-time pads

Note that the longer the key is in the Vignère cipher, the harder it is to break (provided the key-string isn't a well-known text, like the Gettysburg address or Hamlet's soliloquy). A one-time pad is essentially a Vignère cipher with an infinitely long, preferably random, key. Theoretically, this provides an unbreakable cryptosystem, because deciphering part of the message gives no information about the rest. The catch is that, to decode it, you must know what the infinitely long random sequence the message was encoded with.

Such systems were used by spies, where agents were furnished with codebooks containing pages and pages of random characters. Then the key to the encryption is given by the page on which to begin. It is, of course, important that each page be used only once (hence the name ``one-time pad''), because otherwise if a codebreaker were able to intercept a message and (via some other covert means) its corresponding translation, that could be used to decipher messages encoded with the same page. This sort of setup makes sense if an agent in the field is communicating with central command (but not with each other). Each agent is given his own codebook, and he uses one page per message.

A variation on this theme is the ``Augustus cipher'', where instead of a random sequence of shifts, a phrase or passage from a text which is as long as the plaintext is used. The trouble with this is that, because of the regularities in the key, a statistical analysis of the crypttext allows one to break the cipher.

 We can easily modify our Vignere program to be a one-time pad system, using maple's random number generator to make our one-time pad.^3.11 You might think that generating a random sequence of numbers would be inherently unreproducible, so the message would be indecipherable unless we record the ``random stream''. However, computers can not usually generate a truly random sequence. Instead, they generate a ``pseudo-random'' sequence s₁, s₂, s₃,... where the pattern of the numbers s_i is supposed to be unpredictable, no matter how many of the values of the sequence you already know. However, to start the sequence off, the pseudo-random number generator requires a seed-- whenever it is started with the same seed, the same sequence results. We can use this to our advantage, taking the seed to be our key.^3.12 Note that in order to decode the message by knowing the key (the seed), the recipient must use the same pseudo-random number generator.

Maple's random number generator gives different results when called in different ways. If called as rand(), it gives a pseudo-random non-negative 12 digit integer. When called as rand(p), it gives a procedure to generate a random integer between 0 and p; it is this second version that we will use. The seed for maple's random number generators is the global variable _seed.^3.13

 

> OneTimePad := proc(plaintext, keynum)
    local textnum,codenum,i,p,randnum;
    global Alphabet,_seed;
    
    p       := length(Alphabet);
    randnum := rand(p);
    _seed   := keynum;
    textnum := ToNum(plaintext);
    codenum := [seq((textnum[i] + randnum()) mod p, i=1..length(plaintext))];
    FromNum(codenum);
  end:

In this implementation, it is assumed that the key is a positive integer (it can be as large as you like). It would be easy to change it to use a string of characters, however, by converting the string to a number first. One way to do that is discussed in the next section.

In most descriptions of one-time pad systems, one takes the exclusive-or (XOR) of the random number and the integer of the plaintext, rather than adding them as we have done. This does not significantly change the algorithm if the random sequence is truely random, since adding a random number is the same as XOR'ing a different random number. However, the XOR approach has the advantage that the enciphering transformation is its own inverse. That is, if we produce the crypttext using crypt:=OneTimePadXOR(plain,key), then OneTimePadXOR(crypt,key) will give the decryption with the same key. This is not the case for the version given above; to make a decryption procedure, we would need to modify the above by changing the + to a -.

Multi-character alphabets

 We can also improve security a bit by treating larger chunks of text as the characters of our message. For example, if we start with the usual 26-letter alphabet A-Z, we can turn it into a 676-letter alphabet by treating pairs of letters as a unit (such pairs are called digraphs), or a 26³-letter alphabet by using trigraphs, or triples of letters. This makes frequency analysis much harder, and is quite easy to combine with the other crytptosystems already discussed. We will use 99-graphs on a 128-letter alphabet when we implement the RSA cryptosystem in §11.1.

To convert the digraph ``HI'' to an integer (using a length 26<sup>2</sup> alphabet of digraphs), one simple way is to just treat it as a base-26 number. That is, ``HI'' becomes 7*26 + 8 = 190, assuming the usual correspondence of H=7, I=8. To convert back, we look at the quotient and remainder when dividing by 26. For example, 300 = 26*11 + 14, yielding ``LO''.

Below is an example of how we might implement this conversion. We assume our usual functions ToNum and FromNum are defined, as well as the global Alphabet. The routine below converts text into a list of integers, treating each block of k letters as a unit. It is assumed that the length of text is divisible by k.^3.14 A block of k characters c₁c₂c₃...c_k is assigned the numeric value $\sum_{i=0}^{k-1}$x_ikⁱ, where x_i is the value of ToNum(c_i). The only tricky part is getting the right characters in the right position.

> KgraphToKnums := proc(text, k)
     local textnums, i, j, p;
     global Alphabet;
     p:= length(Alphabet);
     
     textnums := ToNum(text);
     [seq( sum( textnums[(j-1)*k + i]* p^(k-i), i=1..k),
           j=1..length(text)/k)];
  end:

This may look a bit impenetrable at first, but when reading it, just keep in mind that j selects which k-block we are looking at, and i is the position of the character within that block.

To undo the transformation, we note that if

X = x₁p^{k - 1} + x₂p^{k - 2} +...+ x_{k - 1}p + x_k,

then x_i $\equiv$ $\left[\vphantom{ X / p^{k-i} }\right.$X/p^{k - i}$\left.\vphantom{ X / p^{k-i} }\right]$ mod p^{k + 1 - i}, where [a] means the integer part of a (that is, we divide and discard any remainder).^3.15 We use maple's iquo function to do the division without remainder.

> KnumsToText := proc(numlist, k)
     local p;
     global Alphabet;
     p:=length(Alphabet);
     FromNum([seq(seq(iquo(modp(numlist[j], p^(k-i+1)),
                            p^(k-i)),
                      i=1..k),
                  j=1..nops(numlist))]);
  end:

In the examples below, we are using the 26-character alphabet discussed above. Of course, this will work on any alphabet.

> KgraphToBignums(`HILOHOLA`,2);

We can also use 4-graphs:

> KgraphToBignums(`HILOHOLA`,4);

> KnumsToText([128740, 132782],4);

Another way to treat multiple characters together is to think of them as vectors. For example, the digraph ``HI'' might correspond to the vector [7, 8]. We will treat this approach in §8.

Footnotes

...tex2html_comment_mark^3.8

This cipher takes its name after Blaise de Vignère, although it is actually a corruption of the one he introduced in 1585. Vignère's original cipher changed the shift amount each letter based on the result of the last encoding, and never repeated. This scheme is much harder to break. However, one reason for its lack of popularity was probably due to the fact that a single error renders the rest of the message undecipherable.

... unbreakable.^3.9

In fact, as late as 1917, this cipher was described as ``impossible of translation'' in a respected journal (Scientific American), even though the means to break it had been well known among cryptographers for at least 50 years.

... -.^3.10

Note that we could also use the Vignere routine, but with the inverse of the key. For example, in the preceding example, the inverse of Prufrock is oMJYMPaT: the numeric code of P plus the numeric code of o is 56 (the length of the alphabet), similarly for r and U, and so on.

... pad.^3.11

Technically speaking, this is not a one-time pad, but a one-time stream. The distinction is subtle, and we will ignore it here.

... key.^3.12

Pseudo-random number generators appropriate for cryptography are rare. Most implementations (including maple's) are good enough for everyday use, but not enough to be cryptographically secure. By analyzing the output of a typical random number generator, a good cryptanalyst can usually determine the pattern. We shall ignore this problem here, however.

....^3.13

We can choose a ``random'' seed (based on the computer's clock) using the function randomize().

....^3.14

See the routine TextToVects in §8.1 for an way around this

... remainder).^3.15

There are more computationally efficient ways of doing this, but we aren't worrying about that.