Enciphering matrices

Treating text as vectors

We can let our enciphering transformation f operate on larger blocks of text than just a single character at a time. However, instead of treating a multi-byte string as a ``super-character'', as in §5.3, we could think of it as a vector of characters. Thus, if we were using, say, 2-vectors, then the name ``Dougal'' might become the three vectors [36, 79], [85, 71] and [65, 76]. If the length of the text we were converting was not divisible by 2, we would have to extend it by adding a space. Thus the name ``Ian'' occurring at the end of a message would become the pair of vectors [41, 65] and [78, 0].

Below is an implementation of this conversion, TextToVects, which takes as input the text to convert to n-vectors and the length of the vectors, n. It uses the ToNum procedure from §4, as well as the usual maple commands.

 

> TextToVects:= proc(text,n)
    local i,j,textnums,vectors;
    
    textnums := ToNum(cat(text, seq(` `,
                                i=1..modp(n-length(text),n))));
    [seq([seq(textnums[(j-1)*n + i], i=1..n)], 
          j=1..nops(textnums)/n)];
  end:

The first thing it does is extend the length of the text to a multiple of n, if needed. This relies on the observation that k + ((n - k)mod n)is a multiple of n, and on the fact that maple will do the right thing with a command like seq(i,i=1..0), that is, produce nothing whatsoever. Then the text, extended by the correct number of blanks, is converted to a list of numbers.

We now parcel up the list of numbers textnums into chunks of size n. This is done by noting that the characters in the j-th vector will come from positions n(j - 1) + 1 through n(j - 1) + n, so the inner seq gives us the j-th vector, as the outer one ranges over all the vectors. If you don't see how this works right off, just take a moment to write out an explicit example for yourself.

Converting back from a list of n-vectors to a character string is easy, because we already have FromNum to convert a list of numbers to a character string for us. All we need to do to change a list of lists to just a list is discard the inner sets of braces. We can use map and op to do this for us:

> map(op,[[36, 79], [85, 71], [65, 76]]);

One small problem is that maple distinguishes between a vector and a list of numbers-- a vector has a little more structure as far as maple is concerned. While we can use the two almost interchangeably (in the same way that we can think of a point in $\mbox{${ \mathbb{ R}}$}$ⁿ as an n-vector, or of as an n-vector as a point), some functions such as op that deal with the internal structure will give different results. So, to be sure that op will work, we need to convert the vectors to lists first. The result is

> VectsToText:= vects -> FromNum(map(op, map(convert,vects,list))):

Affine encoding with matrices

Now that we know how to think of character strings as vectors, we can manipulate them. Our enciphering transformation is just a permutation of the n-vectors.

For example, the Vignère cipher (§5.1) can be interpreted as the applying the map v $\mapsto$ v + b mod p, where vand b are vectors the length of the key.

We can do a more general trick using the affine transformation

v $$\mapsto$$ Av + b mod p

where A is an n x n matrix, and band v are n-vectors. As before, we need certain restrictions on the matrix A. In particular, we need it to be an invertible matrix (so that we can decipher the encoding). This is guaranteed by requiring that the determinant of A be nonzero and share no common factors with p. As before, choosing an alphabet of prime length makes our lives much easier. The linear version of this encoding, v $\mapsto$ Av, is sometimes called a ``Hill cipher''.

In maple, one does matrix arithmetic pretty much as you would expect, except that you need to use &* to indicate matrix multiplication. This is because matrix multiplication is not commutative, while * is. Also, maple doesn't carry out the operations until you execute evalm. Thus, to compute Av + b, we would write evalm(A &* v + b).

> AffineMatEncode := proc(text,A,B)
   local   vtext,vcrypt,i,n,p;
   global  Alphabet;
   
   p:=length(Alphabet);
   n:=nops(convert(B,list));
   
   vtext := TextToVects(text, n);
   vcrypt:= [seq( map(modp,
                      evalm(  A &* vtext[i]  + B),
                      p), 
                  i=1..nops(vtext))];
   VectsToText(vcrypt);
  end:

Note that matricies allow the encodings of nearby characters in the message to interact. For example, we can exchange every other character in a message using the matrix $\left(\vphantom{\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}}\right.$$\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}$ $\left.\vphantom{\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}}\right)$:

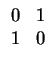
> AffineMatEncode(`I'm so mixed up¡, [[0,1],[1,0]], [0,0]);

To decode a message encoded using A, b, we can encode the crypttext with the matrix A^-1 and the shift vector - A^-1b. You should check for yourself why this is the proper transformation. To obtain the inverse matrix in maple, you can use inverse. This is part of the linear algebra package, so you must either first issue the command with(linalg,inverse) or refer to the function as linalg[inverse].

> A := matrix([[67, 23], [69, 81]]); B:=[5, 47];

> AffineMatEncode(`Lester Hill`,A, B);

> AffineMatEncode(`nG=a/$TvPuUU`, inverse(A), evalm(-inverse(A) &* B));

A Known-plaintext attack on an affine matrix cipher

As in §7.3, we can determine the key if we know what certain characters correspond to. If the message is encoded using n-vectors, we will need to know the decodings for n + 1 vectors, that is, n(n + 1) characters. We then solve the n + 1 vector equations simultaneously to find out the deciphering matrix and shift vector.

We will give a small example: Suppose we receive a message that we know was encoded using an affine cipher on 2-vectors, in our usual 97-letter alphabet. Suppose we also know that the plaintext ``secret'' corresponds to the crypttext ``oHyeAH''. This is sufficient information to decipher the message, because we know the encodings of three different 2-vectors.

> plain:=TextToVects(`secret`,2);

> crypt:=TextToVects(`oHyeAH`,2);

These three vectors give us three equations to solve:

Ac₁ + B $$\equiv$$ p₁        Ac₂ + B $$\equiv$$ p₂        Ac₃ + B $$\equiv$$ p₃

where the c_i are the crypttext vectors and the p_i are the corresponding plaintext, and the equations are taken mod 97. (If this seems backwards, remember we are trying to find the deciphering transformation.) If the code were linear, then the deciphering matrix would be PC^-1, where P and C are the matrices whose columns are made up of the vectors p_i and c_i respectively.^3.18

Since the code is affine, we can either play around manipulating matrices, or we can just translate everything into 6 linear equations in 6 variables. We will take the latter approach.

> A:=matrix([[a,b],[c,d]]); 
  B:=[e,f];

Note that we wish to solve Ac_i + B $\equiv$ p_i (mod 97) for A and B. If we execute the statement evalm(A &* crypt[i] + B - plain[i]), we will get a vector which should be the zero vector. For example, using the first sample, we obtain

> evalm( A&*crypt[1] + B - plain[1]);

This gives us a vector of two expressions we would like to set to zero. If we do this for all three of our samples, and unwrap the vectors using op and convert( ,list), we will get a system of equations appropriate to solve:

> eqns:= seq(op(convert(
  	          evalm(A&*crypt[i] + B - plain[i]),
                    list)), i=1..3);

Now, we use msolve to find out the decoding matrix and shift vector.

> Answer:= subs(msolve(eqns,97),[evalm(A),B]);

We can decode our message now, by encoding the crypttext using the matrix A and shift B found above. A is the inverse of the matrix used for encoding, and B is A times the negative of the original shift vector.

Footnotes

... respectively.^3.18

You probably want to check that this works for yourself.