The RSA Public key cryptosystem

In 1978, R. Rivest, A. Shamir, and L. Adelman published the description of the RSA public key system, which we will describe here. As discussed in §9.3, a public key system allows anyone to encode messages that only the intended recipient may decode. This algorithm relies on the fact that unless one knows some special facts about n, calculating the Euler $\varphi$-function $\varphi$(n) is as hard as factoring n, which, for very large n (say, 200 digits), is very hard indeed.

To set up the system, we pick at random two large primes p and q, of about 100 digits each. We then compute the base n as the product of pand q. Note that $\varphi$(n) = (p - 1)(q - 1). We also pick some other large number a < min(p, q), called the exponent, which is relatively prime to $\varphi$(n). We make the numbers (n, a) public-- these form the key needed for encoding. We also use the Euclidean algorithm to compute xwhich satisfies ax - y$\varphi$(n) = 1; that is, so that $\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{ax}}\right]\kern-.32em\right]}_{\varphi(n)}$}$ = 1. The number x is the part of the key we keep private.

To encode a message: The sender divides his message up into blocks of length k, and to each block assigns an integer $\beta$ (for example, by treating the characters of the message as a k-graph, as in §5.3, with 0$\le$$\beta$ < min(p, q). For each block of plaintext, the sender transmits $\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta^a}}\right]\kern-.32em\right]}_{n}$}$ = m.

To decode the message: For each unit m of the crypttext received, the recipient computes $\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{m^x}}\right]\kern-.32em\right]}_{n}$}$, which is the integer representing of a k-graph of the message. We can see that this is so, because

$$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{m^x}}\right]\kern-.32em\right]}_{n}$}$$ = $$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta^{ax}}}\right]\kern-.32em\right]}_{n}$}$$ = $$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta^{1+\varphi(n)y}}}\right]\kern-.32em\right]}_{n}$}$$ = $$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta}}\right]\kern-.32em\right]}_{n}$}$$$$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta^{y\varphi(n)}}}\right]\kern-.32em\right]}_{n}$}$$ = $$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta}}\right]\kern-.32em\right]}_{n}$}$$$$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{ \left(\beta^{y}\right)^{\varphi(n)}}}\right]\kern-.32em\right]}_{n}$}$$ = $$\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\beta}}\right]\kern-.32em\right]}_{n}$}$$ ^. 1.

This relies on Euler's theorem, so that $\mbox{$\displaystyle{\left[\kern-.32em\left[{\mystrut{\gamma^{\varphi(n)}}}\right]\kern-.32em\right]}_{n}$}$ = 1, where $\gamma$ = $\beta^{y}_{}$. The requirement that $\beta$ be less than both p and q was to ensure that gcd($\beta$, n) = 1, so that we can apply the theorem.

Note that the symmetry between a and x means that we can make either one public. Thus, RSA works just as well for authentication as it does for public key encryption.

   
Implementing RSA in Maple

Now that we have covered how the RSA system works in theory, it is fairly simple to implement it in maple.

Useful preliminaries

First, we define a procedure which allows us to read in a file, and convert it into a list of large integers. This is done using readbytes to obtain chunksize bytes from the file. Each byte is represented by its ASCII code^3.24 (that is, as an integer between 0 and 127), and each group of chunksize characters is viewed as a number expressed in base 128^chunksize. We convert each of these numbers to decimal, as in §5.3. The result is a list of several rather large integers representing the contents of the file. The choice of chunksize is fairly arbitrary, provided you ensure that 128^chunksize is less than your chosen primes. Here we use 47, which gives us 99 digit numbers, because 128⁴⁷ is a 99-digit number.

> Chunksize := 47:
  ReadBignums:= proc(filename,chunksize)
    local file,chunk,i,p,numlist;
    
    p       := 128;
    numlist := [];
    file    := fopen(filename, READ, BINARY);
    chunk   := readbytes(file,chunksize);
    while (chunk <> 0) do
        numlist := [op(numlist), 
                    sum( chunk[i]* p^(chunksize-i), i=1..nops(chunk))];
        chunk := readbytes(file,chunksize);
    od;
    close(file);
    RETURN(numlist);
  end:

For example, if we read in the contents of the file /home/mat331/data/Extra using 47-byte chunks, we obtain a list of 39 numbers of 99 digits each.

> data:=ReadBignums(`/home/mat331/data/Extra`,Chunksize):

> nops(data);

> data[2];

It will also be useful for us to be able to convert our big integers back into text, so that we can read our message when we are done.^3.25

> BignumToText:=proc(num,k)
    local i,p;
    p:=128;
    convert([seq(  iquo(modp(num,p^(k-i+1)),p^(k-i)), i=1..k)],'bytes');
  end:

> BignumToText(data[2],Chunksize);

Basic Setup: choice of primes, base, exponent, and decoding exponent

We wish to choose two primes p and q of about 100 digits each ``at random'', and also a random exponent relatively prime to $\varphi$(pq). At first, this may seem to be a very hard task: how do you know if an arbitrary 100-digit number is prime unless you try to factor it? However, there are a number of efficient ways to test if a number is prime without actually determining its factors. Maple's isprime function uses such methods. Thus, all we really need is to generate some random numbers of about 100 digits, then take the next prime bigger. We use Maple's rand to create two functions, BigRand and MedRand, which give us random numbers of around 100 digits and less than 90 digits, respectively. We also have to remember to use randomize() to ensure that we get a different random number each time (see the discussion of pseudo-random numbers in §5.2, page ).

> BigRand := rand(10^100..10^105):
  MedRand := rand(50..10^90):

> readlib(randomize)();

Now we pick our primes p and q, set phi to be $\varphi$(pq), and compute our base n = pq.

> p:=nextprime(BigRand());
  q:=nextprime(BigRand());
  phi:=(p-1)*(q-1);
  n:=p*q;

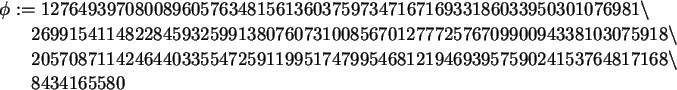
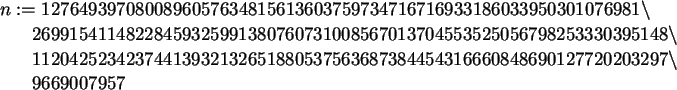
To choose our public exponent a, we pick a number at random and check if it is relatively prime to $\varphi$(n). If not, we just pick another and try again. Usually, a suitable exponent will be found after only a few tries.

> a:=MedRand();
  while( gcd(a,phi) <> 1) do;
      a:= MedRand(); 
  od;

Finally, we choose x to be the inverse of a mod  $\varphi$(n).

> x:= modp( 1/a, phi);

Encoding and Decoding

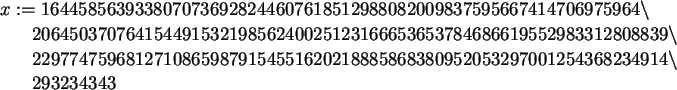
We've already done all the hard work; now writing the actual encoding and decoding routines is easy. Lets write RSAEncodeNum which encodes a single large number $\beta$ by computing $\beta^{n}_{}$mod  n.

> RSAEncodeNum := proc(bignum, a, n)
    modp( bignum &^ a, n);
  end:

> RSAEncodeNum(data[1],a,n);

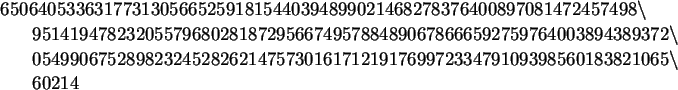
We can easily write a one-liner to encode a file with RSA by using map to apply RSAEncodeNum to the result of ReadBignums.

> RSAEncodeFile := proc(file, a, n)
    map(RSAEncodeNum, ReadBignums(file,Chunksize), a, n)
  end:

> encoded := RSAEncodeFile(`/home/mat331/data/Extra`, a, n):

The variable encoded contains a list of several large integers. This is our message, suitably encoded and ready for transmission to our recipient, but indecipherable to anyone who doesn't know the the inverse of a modulo n, that is x.

The receiver of the message can decode it by using RSAEncodeNum with x in place of a (the recipient doesn't know a). Since this is a list of numbers, the recipient applies BignumToText to convert it back into readable text.

> decoded := map(RSAEncodeNum, encoded, x, n):

> cat(op(map(BignumToText,decoded,Chunksize)));

Footnotes

... code^3.24

We assume here that the data in the file is plain text. If it is expected that there may be extended ASCII codes in the file (or if the file contains ``binary data'', for example, if it is compiled computer code or an image), the variable p should be set to 256 instead.

... done.^3.25

Of course, if you anticipate 8-bit data in your input, the number p here will need changing, as well.