• Intuitive idea of topology
• Point-set topology in the Euclidean space; relation to analysis
• Abstract point-set topology, open and closed sets
• Topological properties (compactness, connectedness)
• Surfaces: definition, examples
• Cut-and-paste arguments for surfaces
• Idea of classification (with some proofs if time permits)
• Euler characteristic

As this is an upper-level class, familiarity with proofs is expected. You will have to write careful proofs in your homework.

L. Christine Kinsey, Topology of surfaces.

Midterm II: Wednesday, November 5, in class.

Midterm I: Friday, October 3, in class. Checklist of topics for Midterm I is here.

No make-up exams will be given for midterms. If a student misses a midterm exam for a well-documented medical reason or other similar circumstances beyond the student's control, the student may be excused from the exam, with the final grade determined from the other exams, homework, and class participation. For the final exam, make-ups will be given ONLY in cases of properly documented medical reasons or other similar circumstances, at the instructor's discretion.

Important: For each homework problem, please give a proof or detailed explanation as appropriate (unless otherwise stated). Please write up your solutions neatly, be sure to put your name on the first page and staple all pages. Illegible homework will not be graded. You are welcome to collaborate with others and to consult books, but your solutions should be written up in your own words, and all your collaborators and sources should be listed. Reading assignments for each week are to be taken very seriously -- even if you understood the material in class, being able to follow a proof in a book is an important skill. You will often be required to "read ahead" on some material, both to prepare for class and to sharpen your math reading skills.

Week 1 (08/25 – 08/29) Read sections 1.1, 2.1 (up to Definition 2.10).
Homework 1, due Sept 3: please do the exercises from the book listed below, as well as a quick review of sets, and a topological experiment:
1.1 (use your intuition; no explanations required);
2.1 and 2.3 (parts 4-8 only for both exercises; do only "open" and "closed" questions for 2.1, ie skip "bounded"). Explain your answers.
2.7, 2.9, 2.10 (give proofs).
Also, recall MAT 200 material and determine which of the following identities are true:
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
(A ∩ B) ∪ C = (A ∩ C) ∪ (B ∩ C)
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C). Give proofs or counterexamples to support your answer.
For the experiment, recall that a Mobius band can be made from a long rectangular strip of paper: just glue the ends of the strip after a half-twist. We played with these in the first lecture; we learned that the Mobius band has only one side (unlike the case of a usual annular strip with no twist, you cannot color one side red and the other blue). Also, you do NOT get two halves if you try to cut the Mobius band in half along its length.
Repeat the second experiment at home and examine the (single) band you get when you cut the Mobius band along its length. Do you think you get a Mobius band? Why or why not?
Repeat the Mobius band experiments (coloring and cutting) for a band obtained by gluing the ends of a rectangular strip after 2 half-twists (i.e. one full twist). Describe the results. Can you predict what would happen if you tried to make similar experiments for a band with 2014 half-twists? 2015 half-twists?

Week 2 (09/3 – 09/5) Read sections 2.1, 2.2, begin 2.3.
Homework 2, due Sept 10: please do the exercises from the book listed below. Work carefully from the definitions, write detailed proofs.
2.4, 2.6, 2.8, 2.12, 2.15, 2.16, 2.21, 2.23

Week 3 (09/8 – 09/12) Read sections 2.2, 2.3.
Homework 3, due Sept 17: please do the following two exercises from the book, as well additional questions below.
2.22, 2.25. (As always, argue carefully from definitions/theorems. For 2.25, be sure to work with definition 2.15.)
Q1. Suppose A, B are subsets in Rⁿ, such that B is contained in A. Show that if B is closed, then B is closed relative to A.
Q2. Show that a constant function (on any domain) is always continuous. Argue from definition 2.15!
Q3. Consider the set P={1, 2, 3} (i.e. P consists of three points in the real line). Prove (from definition!) that any function f: P → P is continuous.
Q4. Consider the set E= {1/2, 2/3, 3/4, 4/5,....,n/(n+1),...} in the real line. Is E closed? Is E closed relative to (0,1)? Is E closed relative to [0,1]? Prove your answers carefully.
Q5. Let Q be the set of rational real numbers. Give an example of a subset B in Q such that B is neither open nor closed in the real line, but is both open and closed relative to Q.

Week 4 (09/15 – 09/19) Read section 2.3 again. Ignore part (2.16) but pay special attention to homeomorphisms/topological equivalence toward the end of the section. Read section 3.1 and the first page of 3.2. Keep in mind that our approach to topological spaces is slightly different: we just say that a topology on a set is a chosen collection of "open subsets" satisfying properties from Theorem 3.5. (We will later explain how to build a topology from a "basis", but for now ignore Definition 3.4.)
Homework 4, due Sept 24: please do the following exercises from the book, as well additional questions below. 3.3, 3.4, 3.9, 3.10. In 3.10 (2), you are asked to give an example where A or/and B is not closed, and the resulting function is NOT continuous.
Q1. Show that the open interval (0,1), the open ray (0, + ∞), and the line (- ∞, +∞) are all homeomorphic. Think back to familiar functions from analysis/calculus to find homeomorphisms; use Theorem 2.17 to justify continuity. (You DO NOT have to argue with open sets for this question.)
Q2. Let f:Rⁿ → Rⁿ be continuous (with respect to the usual Euclidean space topology). Let X be some subset of Rⁿ, and define the function g: X → Rⁿ by g(x) = f(x) for all x in X. (Such g is called a "restriction" of f; it works in exactly the same way, except on a smaller domain.) Show that g is continuous.
Q3. Consider f: X → Y, where X and Y are some topological spaces. Show that f is continuous whenever (a) X has discrete topology, OR (b) Y has indiscrete topology.
Q4. Let Y={a, b, c} be a three-point set, with topology {∅, {a}, {a, b}, {a, b, c}}. Give an example of a non-constant continuous function f:[0, 1] → Y, where [0,1] has its usual topology given by relatively open sets. Justify continuity carefully. Will your function remain continuous if instead you take discrete topology on {a, b, c}? Why?

Solutions to Homework 4 (written by Joe Thurman) are here. Joe's solution of Question 3.3 is very long because he did a very careful analysis of all possible cases. You'd get fewer topologies if you only count those that give "different" pictures; for example, topologies T₂, T₃, T₄ all look the same. An acceptable solution would list a number of topologies along with a quick checking that each of them is indeed a topology. In question 2, Joe wrote a careful MAT 319-style proof of continuity; you could get away by saying that we know from analysis that every rational function is continuous on its domain, the exponential function is continuous, etc. (By equivalence of different definitions of continuity, these functions are continuous in the "topological" sense as well.)

Homework 5, due Oct 1, is posted on Blackboard due to technical issues. Solutions to Homework 5 (by Joe Thurman) are here.

Week 6 (09/29 – 10/3) Connected spaces (Definition (3.14)). We looked at some simple examples (it is typically easier to prove disconnectedness than connectedness) and proved an important theorem: a closed interval [a,b] is connected. (As a quick corollary, we also proved that an open interval (a, b) is also connected.)

Homework 6, due Oct 8: Please do questions 3.11, 3.12 , as well as additional questions below:

Q1. Using the fact that any closed interval is connected, show that the line is connected, that any ray (a, + ∞) and [a, + ∞) is connected, and that half-open intervals [a, b) and (a, b] are connected. Your proofs should all be very similar and quite short.

Q2. Consider the collection B of all intervals of the form (a, b] on the real line R. Prove that B is a basis for some topology on R. Is this the usual (standard Euclidean) topology on the line? Is the interval (0,1] connected in this topology? Prove your answers.

Q3. Consider the space X={a,b,c,d,e} with topology T= {{a,b}, {d,e}, {a,b,d,e}, X, ∅}. Is X connected? Prove your answer.

Homework 7, due Oct 15: Please do exercise 2.31 from the book (with proof), as well as the following questions:

Q1. Consider a set X={a, b, c, d} consisting of four points. Give examples of
(1) two different topologies on X such that the resulting topological spaces are both connected but not homeomorphic;
(2) two different topologies on X such that the resulting spaces are both disconnected but not homeomorphic to each other.
This is a straighforward but long question, you have to (i) come up with examples, (ii) show that your topologies are actually topologies, (iii) show that corresponding spaces are connected/disconnected, as required, (iv) show that your two connected spaces are not homeomorphic to each other, and same for disconnected.

Q2. In class, we proved the following lemma:
If X = U ∪ V where U, V are connected and intersect non-trivially, i.e U ∩ V ≠ ∅, then X is connected.
Using this lemma, prove that the letters K, H, E, A (considered as subspaces in the plane with the usual topology) are connected.

Q3. Prove the following statement (it generalizes the lemma above). Suppose we are given a number of connected subsets (perhaps infinitely or even uncounably many) of some space X, such that all these subspaces contain a given point z. Show that the union of these spaces is connected. (Think carefully about the proof we gave in class, and you'll see that similar proof works for this case.)

Q4. Let W be a subset of Rⁿ with the usual topology (think n=2 if that's easier). Suppose that any two points in W, the straight line segment connecting those points lies in W. (In this case, W is called "convex"). Prove that W is connected. (Hint: suppose not, then W breaks into disjoint union of non-empty open subsets. Pick a point from each and connect them by a segment.)

Q5. Determine (with proof) which of the following spaces are connected. (For disconnected, the proof would just be to break your space into two open subsets. To prove that a space is connected, you can use all the preceding questions.) The first four spaces are subsets of the plane (with usual topology).
(i) the plane;
(ii) a disk D²(x, r);
(iii) the plane with a line removed (eg remove the x-axis from the coordinate plane);
(iv) the plane with a point removed (eg remove the origin);
(v) the set of rational numbers (with its topology as a subset of the real line).

Solutions to Homework 7 (by Joe Thurman) are here.

Week 8 (10/13 – 10/17) We continued working with connected and disconnected spaces, covering a few topics that are not in the textbook: showing that a space is connected via path-connectedness; connected components; using the property of connectedness/disconnectedness to show that some spaces cannot be homeomorphic. (A trick that we used: remove a point - or several - from one of your spaces. Does it remain connected? How many connected components can you get? If the two spaces are homeomorphic, removing the "corresponding" (via the possible homeomorphism) point(s) from the second space should give the same number of connected components.)

Notes on connectedness are here. (Updated 10/17 at 11am.)

Homework 8, due Oct 22: please do the questions below.

Q1. What's wrong with the following argument:
Suppose X is a subset of R², and X is not connected. Then X = A ∪B, where A and B are open, disjoint, and non-empty. We know that the union of two open sets is always open, so X must be open. Therefore, any subset of the plane which is NOT open must be connected.
To disprove this argument,
(a) Give an example of a non-open subset of the plane (with the usual topology) which is not connected. (Justify all your statements.)
(b) Pinpoint the mistake in the paragraph above - explain what exactly goes wrong in the proposed argument.

Q2. When trying to prove that a space is path-connected, it's important to be able to construct paths. A path in X is a continuous map γ [0,1] → X; its endpoints are points a=γ(0) and b=γ(1). (Instead of [0,1], one can consider any closed interval, as the intervals can be reparameterized: for example, given a path γ(t), 0 ≤ t ≤ 1, set s=t+1 to get a path γ': [1,2] → X, with γ'(s)= γ(s-1).)

Show that if you have a path from a to b, and another path from b to c, these paths can be joined to form a path from a to c. Namely, suppose X is some topological space, γ₁ :[0,1] → X and γ₂ :[1,2] → X are paths such that γ₁ (1) = γ₂ (1). Define δ[0,2] → X by δ(t) = γ₁(t) if t ≤ 1 and δ(t) = γ₂(t) if t > 1.
Prove that δ is continuous.
This looks like a long question, but in fact you are only asked to prove that a particular map is continuous. X can be any space; please work from the topological definition of continuity.

Q3. How many connected components does each of the following spaces have? (They are all subsets of the plane with the usual topology) Identify the components and justify your answers carefully. (You will need to show that your components are connected (and disjoint), and that each is both open and closed in your space. To prove connectedness, you can use any of the techniques we developed, including path-connectedness.)
(a) The (x,y)-plane with a circle {x² +y²=1} removed
(b) The (x,y)-plane with a ray removed. (For concreteness, remove the positive part of the y-axis, ie L={(0,y), y>0}.)
(c) The (x,y)-plane with both the positive and the negative parts of the x-axis removed (the origin is not removed). (That is, we remove all (x,0) with x ≠ 0.)

Q4. Prove that letters A and P are not homeomorphic. (Assume that the letters - block capitals - are written on a piece of paper and considered as subsets of R² with the usual topology.)

Q5. Recall that we defined a topology on a product X x Y of two topological spaces X and Y: the basis of product topology is given by the collection of all possible products U x V of open sets in X and open sets in V. (This is definition 3.28 in the book.)
Fix a point y in Y. Prove that the slice X x {y} is homeomorphic to X. (This is an easy question, but you have to figure out the topology on X x {y} - we consider X x {y} as a subset of X x Y, with a subspace topology given by relatively open sets.)

Q6. Suppose that X and Y are connected. Prove that X x Y is connected.
Hint: argue by contradiction. Suppose X x Y is a union A ∪ B of two disjoint open sets. Pick a point (x,y) from A. Show that the entire "horizontal" slice X x {y} must lie in A. Then show that every "vertical" slice {a} x Y (for any a in X) must also lie in A. (Use the lemma from previous homework.) But then you get that all of X x Y lies in A, and B must be empty!

Q7. Suppose that X and Y are path-connected. Show that X x Y is also path-connected.
(You cannot derive this from Q6 as a connected space might NOT be path-connected. Instead, argue directly: you just need to connect any two points (a,b), (c,d) by a path in X x Y.)

Week 9 (10/20 – 10/24) The topics for this week is the Hausdorff property and compactness. Hausdorff is a short topic; all you need to know (and more) is in 3.3. Compactness is a lot more important, and there's more to discuss. We work with definition 3.17 in 3.2 (NOT with the sequential compactness definition in 2.4, although 2.4 is recommended reading as well). So far, we looked at examples of compact and non-compact spaces, and showed that a compact subset of Rⁿ must necessarily be closed and bounded. (Note that the proof we gave in class used open covers and is DIFFERENT from the one in 2.4.). For compactness questions in this homework, please WORK DIRECTLY FROM DEFINITION 3.17.

Homework 9, due Oct 29: please do questions 3.15, 3.16, 3.22, 3.25, 3.26 from the book, as well as two additional questions below.
Hint for 3.25: choose disjoint neighborhoods for each y from Y and the point x. Show that all these neighborhoods for different y's form an open cover for the set Y. Then you an choose a finite subcover (why?) Now use the finite collection of the neighborhoods you get to form the required set V; also, use the corresponding neighborhoods of x (you were looking at different neighborhoods of x for different y's!) to make the set U.
3.26 is a quick corollary of exercise 3.25 if you think carefully about what it means to be closed.
Q1. Suppose f: X → Y is a continuous function which is onto.
(a) If X is Hausdorff, must Y always be Hausdorff?
(b) If Y is Hausdorff, must X always be Hausdorff?
Prove or give a counterexample.
Q2. Let A= {1, 1/2, 1/3, 1/4,...1/n...}, B={0, 1, 1/2, 1/3, 1/4, ...1/n...}. As topological spaces, A and B have the subspace topology (given by relatively open sets) that comes from the usual topology on R.
Is A compact? Is B compact? Please argue directly from the open covers definition (3.17). DO NOT use the closed and bounded criterion.

Solutions to Homework 9 (by Joe Thurman) are here.

Week 10 (10/27 – 10/31) Compactness. We developed further properties (Theorems 3.18, 3.19 in the book) and showed that a closed and bounded subset of Rⁿ is compact. (For that, we can simply show that a "block" [a₁, b₁]x [a₂, b₂]x ...x[a_n, b_n] is compact and use Theorem 3.18.) Our proof that this "block" (and the interval [a,b]) is compact was in terms of open covers (unlike the proof in Ch.2). Sketch proof: first use analysis to show that that every sequence has a convergent subsequence. (We did this by showing that any sequence of real numbers has a monotonic subsequence; if you're in [a,b], you get a monotonic and bounded subsequence, so it converges (to a point of [a,b]). In more dimensions, choose convergent subsequences in each coordinate.) Second, we assumed that there exists a cover with no finite subcover, chose a special sequence "escaping" from sets of the cover, and got a condradiction with convergence of subsequence.) I will try to post lecture notes later; meanwhile, your class notes should suffice.

Homework 10, due Nov 5: see questions below.
In class, we defined convergent sequences in an arbitrary topological space: {x_n} converges to z if for any given neighborhood U of z (ie an open set containing z) there exist N such that x_n lies in U for all n>N. (Clearly, this generalizes familiar definition from analysis: take U = (z-ε, z+ε).) Note that as in analysis, it's okay to consider sequences with repeating terms (a sequence is not a set!)
Q1. Suppose that X has indiscrete topology. Show that any point a in X is the limit of any sequence {x_n}. This tells you that in a general topological space, a sequence can have many limits -- the limit is no longer unique!
Q2. Suppose that X is Hausdorff. Show that a sequence of points of X can have no more than one limit. (That is, uniqueness of limits holds in Hausdorff spaces!)
Q3. (updated!) Let X be any topological space, and {x_n} a convergent sequence in X. Show that the set of points of the sequence, together with the limit, is a compact subset of X.
Q4. Let A be a subset of Rⁿ, with usual topology. Recall the definition of closure Cl A (definition 2.8 in the book). Arguing from this definition, show that
Cl A = {z: z = lim x_n for some sequence {x_n} of points of A}.
Q5. Let X be any topological space, A, B compact subsets of X. Is A ∪ B always compact? Prove or give a counterexample.
Q6. Recall that half-open topology on R has a basis given by all intervals of the form (a, b] (see Q2 of HW 6 and discussion at bottom of p.41 in the book). Consider [0,1] with this topology (ie the subspace topology you get from the half-open topology on R). With this topology, is [0,1] compact? Prove your answer.

Week 12 (11/10 – 11/14) Please read sections 4.1 and 4.3. (4.1 has some material on cell complexes that we won't discuss for a while; focus on planar diagrams and intrinsic vs. extrinsic properties.) So far, we have discussed part of 4.3 and will finish it by the end of the week.

Homework 11, due Monday, Nov 17:
4.11 (give a precise proof),
4.10 (you don't have tools for a precise proof, but do include some explanation),
4.4 (find the surface that's different from the rest, give some explanation; show that all the rest are homeomorphic)
4.22 (answer "which surface" question by using some connected sum, similarly to Q1 below.) Do Q1, Q2 below
Also do Q3, 4.9, 4.12 . All of these three questions use the same idea; please so them after Wednesday (we need to cover more material).
Q1. As we discussed in class, one only cuts out one disk out of each surface when making a connected sum, so the picture does not represent a connected sum of S and the torus. What does the picture represent? (Give the answer in terms of some connected sum, perhaps of S with another surface, or perhaps connect-summing several times. Justify your answer.)
Q2. Suppose M, N, and S are each a connected surface. Show that their connected sum does not depend on the order of summing: for example, (M # N) # S = (S # M) # N, etc. (Note that this isn't entirely obvious - you could attach S to M or to N, and you need to show that such a choice doesn't affect the result, up to a homeomorpism.)
Q3. Show that if you attach a disk to the Mobius band, so that the boundary circle of the disk is glued to the boundary circle of the Mobius band, you will get a projective plane. (Recall that unlike cylinder, the Mobius band has only one boundary circle. Id this doesn't make sense, make a paper model and see for yourself.) To solve this question, argue from planar diagrams: cut out a Mobius band out of a diagram for P, and show that the remainder will be a disk.
For most questions of this homework, some "arguing from picture" will be necessary - it won't be possible to write a formula for a homeomorphism. Try to be as precise as you can, though, and remember that "cut-and-paste" arguments are valid proofs (as long as you follow conventions).

Week 13 (11/17 – 11/21) Please read sections 4.4, 4.5 and 4.6. (4.4 has some material that we didn't cover; you can skip those parts if they don't make sense. Skip Tietze's transformations in 4.5.)

Homework 12, due Monday, Nov 24: 4.19, 4.21, 4.26, 4.27 (1). In 4.21, you'll need to go through (at least some) of the steps of the classification proof. For grading purposes, each part of 4.21 will be treated as a separate question. In 4.27, the surface is made out of the triangles listed (so that, for example, the side CH of triangle BCH is glued to the side CH of triangle CDH).

Weeks 14-15 (11/24 – 12/05) Euler characteristic. Definition for triangulated surfaces and, more generally, for cell complexes. Calculations for all closed surfaces. Topological invariance of the Euler characteristic (for now we are taking it for granted, as we haven't checked that χ is independent of triangulations. Some proofs, at least for the sphere, will be discussed next week). Upshot: we can (sometimes) use χ to prove that two spaces are not homeomorphic!
Please read section 4.2 (we need the definition of cell complexes and basic examples; skip the more technical part), section 5.4, and section 5.3. (Most of the 5.3 material will be discussed next week.)
Homework 13, due Wednesday, Dec 3:
Q1. Recall homework question from the beginning of the course, Exercise 1.1 in the book (classifying block capitals A, B, C,... up to homeomorphism). Check what the Euler characteristic can tell us for this question:
(a) Find three letters with different Euler characteristics (so that χ tells you that no two of these letters can be homeomorphic.)
(b) Find two non-homeomorphic letters with the same Euler characteristic (so that χ fails to see the difference). You will need to use other methods (from earlier in the course) to show that the letters you picked are non-homeomorphic; please outline the proof.
For purposes of this question, treat letters as 1-dimensional cell complexes -- indeed, they can be built with vertices (0-cells) and edges (1-cells).
Q2. For closed surfaces, once we have the classification theorem, an arbitrary surface can be identify by (i) checking its orientability, to find out whether it is a connected sum of tori or a connected sum of projective planes, and (ii) computing the Euler characteristic to find out how many tori (resp. projective planes) were summed. Use this strategy to identify surfaces from Exercise 4.21 (1)-(3) (the last part was done in class). Check your answers from HW 12!
Q3. Extend the strategy described in Q2 to the case of surfaces with boundary. (You can figure it out yourself, extract it from section 5.4, or just wait until we discuss it in class on Monday.) Use this strategy to identify surfaces in 4.27 (2)-(4). Also, use the direct examination/cut-and-paste strategies to identify the same surfaces by different means. (Make sure you get the same answers!)
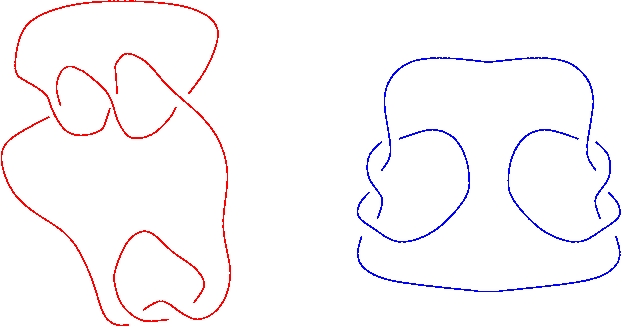
Q4. Identify the two surfaces shown in the figure. As in Q3, use the classification of surfaces along with the Euler characteristic.
Q5. Let M and N be two surfaces with Euler characteristics χ(M) and χ(N). Find (with proof) the Euler characteristic of the connected sum M#N.

Students with Disabilities: If you have a physical, psychological, medical or learning disability that may impact your course work, please contact Disability Support Services, ECC (Educational Communications Center) Building, room 128, (631) 632-6748. They will determine with you what accommodations, if any, are necessary and appropriate. All information and documentation is confidential. Students who require assistance during emergency evacuation are encouraged to discuss their needs with their professors and Disability Support Services. For procedures and information go to the following website: http://www.stonybrook.edu/ehs/fire/disabilities

Academic Integrity Statement: Each student must pursue his or her academic goals honestly and be personally accountable for all submitted work. Representing another person's work as your own is always wrong. Faculty are required to report any suspected instances of academic dishonesty to the Academic Judiciary. Faculty in the Health Sciences Center (School of Health Technology & Management, Nursing, Social Welfare, Dental Medicine) and School of Medicine are required to follow their school-specific procedures. For more comprehensive information on academic integrity, including categories of academic dishonesty, please refer to the academic judiciary website at http://www.stonybrook.edu/commcms/academic_integrity/index.html

Critical Incident Management Statement: Stony Brook University expects students to respect the rights, privileges, and property of other people. Faculty are required to report to the Office of Judicial Affairs any disruptive behavior that interrupts their ability to teach, compromises the safety of the learning environment, or inhibits students' ability to learn. Faculty in the HSC Schools and the School of Medicine are required to follow their school-specific procedures.