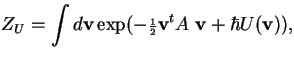

The integrals of interest in Physics have the form
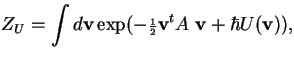
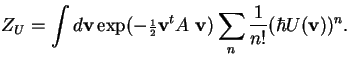
If U is a polynomial in the coordinate functions v1, ...vd, then each term in the sum of integrals is a sum of m-point functions, and can be evaluated by our method, which can be written symbolically as:

Example: This example is formally like the ``![]() theory.'' We take
theory.'' We take
![]() and analyze
and analyze
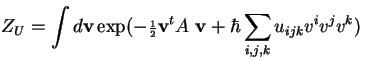
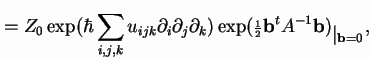
Let us compute the terms of degree 2 in ![]() .
.
These terms will involve 6 derivatives; their sum is:

By Wick's Theorem we can rewrite this sum as
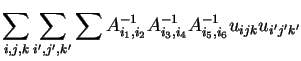
These pairings can also be represented by graphs, very much in the same way that we used for m-point functions: there will be one trivalent vertex for each u factor, and one edge for each A-1. In this case there will be exactly two distinct graphs, according as the number of (unprimed, primed) index pairs is 1 or 3.

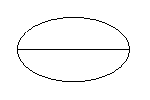
Summing over all possible labellings of these graphs will give some duplication, since each graph has symmetries that make different labellings correspond to the same pairing.
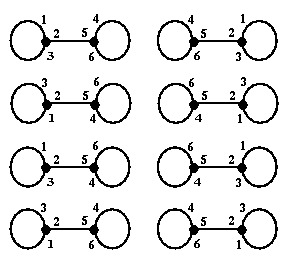
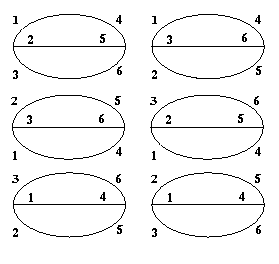
All six of these labelings, and their six left-right mirror images,
correspond to the same product:
u123 u456 A-114 A-125 A-136.
Keeping this in mind, we may rewrite the coefficient of ![]() as:
as:
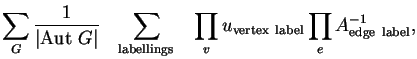
In general, the ``Feynman rules'' for computing the coefficient of
![]() in the expansion of
ZU
are stated in exactly this way,
except that the sum
in the expansion of
ZU
are stated in exactly this way,
except that the sum ![]() is over trivalent graphs with
2n
vertices
(and 3n
edges).
is over trivalent graphs with
2n
vertices
(and 3n
edges).
6. Calculations with a potential function, ``Feynman Rules''
|
|
|
© Copyright 2001, American Mathematical Society |