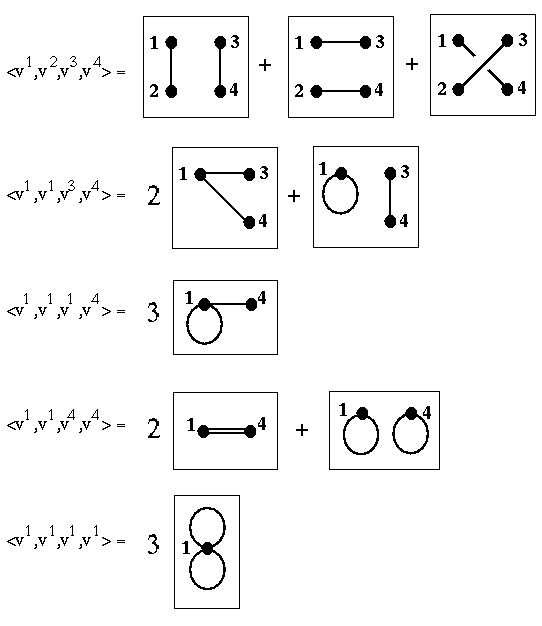

In the last section we calculated some 2 and 4-point functions:
<v1,v2> = A-11,2
<v1,v1> = A-11,1 <v1,v2,v3,v4> = A-12,3A-11,4 + A-12,4A-11,3 + A-134A-11,2 <v1,v1,v3,v4> = 2 A-11,4A-11,3 + A-13,4A-11,1 <v1,v1,v1,v4> = 3 A-11,4A-11,1 <v1,v1,v4,v4> = 2A-11,4A-11,4 + A-14,4A-11,1 <v1,v1,v1,v1> = 3 A-11,1A-11,1It is convenient to represent each of products appearing on the right as a graph, where the vertices represent the indices of the coordinates vi appearing in the m-point function, and each A-1i,j becomes an edge from vertex i to vertex j. Here are the graphs corresponding to the terms in the 4-point functions above.
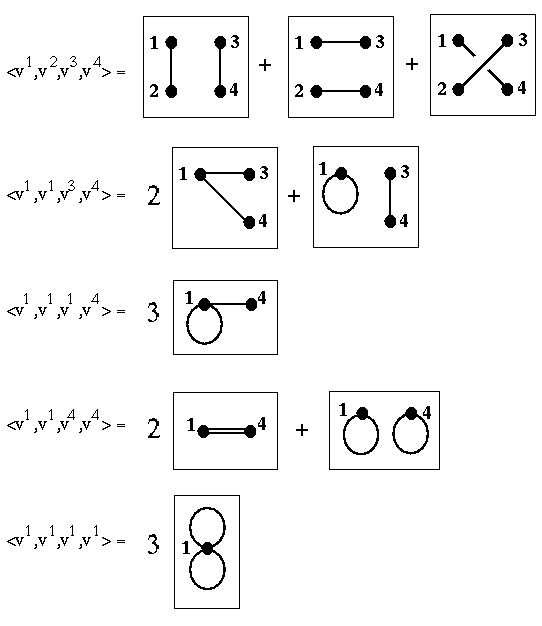
5. The first appearance of graphs
|
|
|
© Copyright 2001, American Mathematical Society |