The basic fact from calculus that powers the whole discussion is:
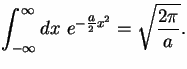
The identity with a = 1
is proved by the trick of calculating the square of the
integral in polar coordinates. The general identity follows by change of variable
from x
to
![]() .
.
This fact generalizes to higher-dimensional integrals. Set v = (v1, ..., vd) and dv = (dv1 ... dvd), and let A be a symmetric d by d matrix.
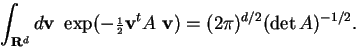
We use the fact that a symmetric matrix A is diagonalizable: there exists an orthogonal matrix U (so Ut = U-1) such that UAU-1 is the diagonal matrix B whose only nonzero entries are b11, ... , bdd along the diagonal. Then A = U-1BU and vtAv = vt U-1B U v = vtUtB U v = wtB w where w = Uv, using Ut = U-1 and (Uv)t = vtUt. Since U is orthogonal detU = 1 and the change of variable from v to w does not change the integral:
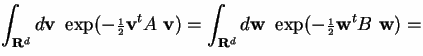
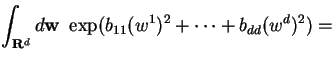
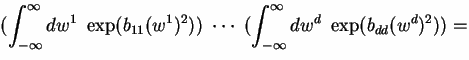
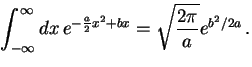
This follows from Proposition 1 by completion of the square in the exponent and a change of variables.
The generalization to d dimensions replaces a with A as before and b with the vector b = (b1, ... , bd)
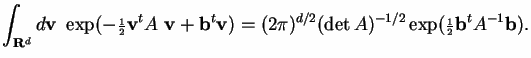
This is proven exactly like Proposition 2. If we write this integral as Zb then the integral of Proposition 2 is Z0 and this proposition can be rewritten as
- 1. What every Freshman should know
2. Facts from calculus and their d-dimensional analogues
- 3. m-point functions
- 4. Wick's Theorem
- 5. The first appearance of graphs
- 6. Calculations with a potential function, ``Feynman Rules''
- 7. Correlation functions
|
|
|
© Copyright 2001, American Mathematical Society |
