Non-Riemannian examples

The present context is certainly not restricted to Riemannian metrics. As an indicator of this we now discuss a different set of examples.

Let k be a positive number greater than one. Equip $\mbox{$\Bbb R$ }^2$ with the distance function

$$\parallel x-y \parallel = \left( \vert x_1-y_1\vert^k + \vert x_2-y_2\vert^k \right)^{1/k}$$

and let the discrete set S be given by $\mbox{$\Bbb Z$ }^2$. For k not equal to 2, this is not a Riemannian metric, yet all conclusions of section 2 hold. In particular, each Brillouin zone forms a fundamental domain. Note that determining the zones by inspecting the picture requires close attention!

  

Figure: Brillouin zones for the lattice $\mbox{$\Bbb Z$ }^2$ in $\mbox{$\Bbb R$ }^2$ with the metric $\left (\vert x_1-y_1\vert^4 + \vert x_2-y_2\vert^4 \right )^{1/4}$. See also Figure 2.3 and Example 2.6, which deal with the case k=1, the ``Manhattan metric''.

Now the problem of determining $C_t(0)\cap S$ for any given t is unsolved for general k. In fact, even for certain integer values of k greater than 2, it is not known whether $C_t(0)\cap S$ ever contains at least two points that are not related by the symmetries of the problem. For k=4, the smallest t for which $C_t(0)\cap S$has at least two (unrelated) solutions is given by

t⁴=133⁴+134⁴=158⁴+59⁴ .

However, for $k \ge 5$, it unknown whether this can happen at all (see [SW]).

There are some things that can be said, however. In the situation where $k\in\left\{{3, 4, 5, \ldots}\right\}$, the mediatrices intersect the coordinate axes only in irrational points or in multiples of 1/2. For if x=(p/q,0) is a point of a mediatrix L_{(0,0),(a1,a2)}, we have

$$\vert p\vert^k = \vert p - q a_1\vert^k +\vert a_2 q\vert^k \quad (p\ne 0, q\ne 0) \quad .$$

By Fermat's Last Theorem, this has no solution unless either p = q a₁ or a₂= 0. In the first case, ${p \over q} = \pm a_2$, which can only occur if the lattice point is of the form $(a_2, \pm a_2)$. If a₂=0, then ${p \over q}={a_1 \over 2}$. In particular, there is no nontrivial focusing along the axes.

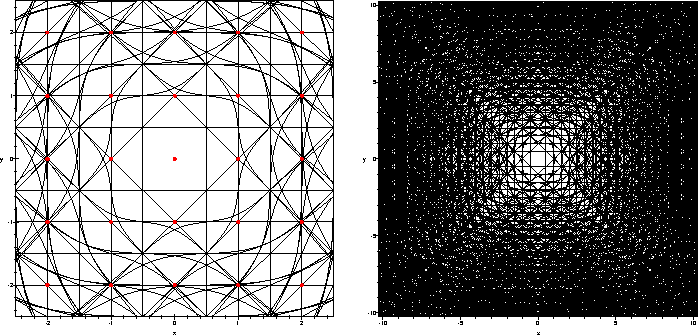
To compute Figure 5.1, we took advantage of the smoothness of the metric. Not all metrics are sufficiently smooth for this procedure to work. Even for Riemannian metrics, in general the distance function is only Lipschitz, which will not be sufficiently smooth.

For each $a=(a_1,a_2) \in \mbox{$\Bbb Z$ }^2$, define a Hamiltonian:

$$H_a(x) = \parallel x-a \parallel - \parallel x \parallel .$$

The mediatrix L_0a corresponds to the level set H_a(x) = 0. Because H_a(x) is smooth, we have uniqueness of solutions to Hamilton's equations. In the current situation, where the dimension is two, the level set consists of one orbit. Thus, one can produce the mediatrix by numerically tracing the zero energy orbits of the above Hamiltonian.

As mentioned above, for a general Riemannian metric, the distance function is only Lipschitz. This means we have no guarantee that the solutions of the above differential equation are unique. Indeed, there are examples of multiply connected Riemannian manifolds with self-intersecting mediatrices, as will be shown in a forthcoming work.