Definitions and main results

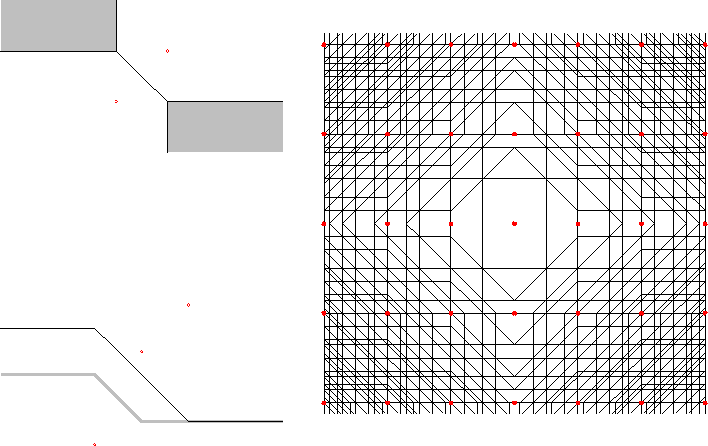
In this section, we prove that under very general conditions, Brillouin zones tile (as defined below) the space in which they are defined, generalizing an old result of Bieberbach [Bi]. With stronger assumptions, we prove that these tiles are in fact well-behaved sets: they are equal to the closure of their interior.

Notation: Throughout this paper, we shall assume X is a path connected, proper (see below) metric space (with metric $d(\cdot,\cdot)$). We will make use the following notation:

• Write an open r-neighborhood of a point x₀ as $${N_r(x_0)= \left\{{ x\in X \,\,\vrule{}\,\,d(x_0,x)<r}\right\} }$$.
• Define the circumference as $${ C_r(x_0)= \left\{{ x\in X \,\,\vrule{}\,\,d(x_0,x)=r}\right\} }$$.
• Their union is the closed disk of radius r, denoted by $${D_r(x_0)= \left\{{ x\in X \,\,\vrule{}\,\,d(x_0,x) \leq r}\right\}}$$.

Definition 2.1   A metric space X is proper if the distance function $d(x,\cdot)$is a proper map for every fixed $x\in X$. In particular, for every $x\in X$and r>0, the closed ball D_r(x) is compact. Such a metric space is also sometimes called a geometry (See [Ca]).

Note if X is proper, it is locally compact and complete. The converse also holds if X is a geodesic metric space (see Thm. 1.10 of [Gr]). The metric spaces considered here need not be geodesic.

Definition 2.2   The space X is called metrically consistent if, for all x in X, R > r >0 in $\mbox{$\Bbb R$ }$, and for each $a\in C_R(x)$, there is a $z \in C_r(x)$ satisfying $${N_{d(z,a)}(z) \subseteq N_R(x)}$$and $${C_{d(z,a)}(z) \cap C_R(x) = \left\{{a}\right\}}$$.

This property is satisfied for any Riemannian metric.

Note that any mediatrix L_a,b separates X, that is: X-L_abcontains at least two components (one containing the point a and the other b).

Definition 2.3   We say that the mediatrix L_ab is minimally separating if for any subset $\tilde{L} \subset L_{ab}$ with $\tilde{L} \neq L_{ab}$, the set $X-\tilde{L}$has one component.

Let L_0a be a mediatrix. If it is minimally separating, then X-L has exactly two components. Also note that if a separating set $L \subseteq X$contains a non-empty open set V, it cannot be minimally separating. For if A and B are disjoint open sets containing X-L, then so are $\tilde{A} = A-(A\cap V)$ and $\tilde{B}=B-(B\cap V)$. Now let x be any point in V. Then it is easy to see that the disjoint open sets $\tilde{A}\cup V$ and $\tilde{B}$ cover X-(L-x). Thus L-x separates.

We define the following sets

$$L_{0a}^-=\left\{{ x\in X \,\,\vrule{}\,\,d(0,x)-d(a,x) < 0 }\... ...^+=\left\{{ x\in X \,\,\vrule{}\,\,d(0,x)-d(a,x) > 0 }\right\}.$$

Definition 2.4   Two minimally separating sets L_0a and L_0b are topologically transversal if they are disjoint, or if for each $x\in L_{0a}\cap L_{0b}$ and every neighborhood V of x, the sets $L_{0a}^+\cap L_{0b}^+\cap V$, $L_{0a}^+\cap L_{0b}^-\cap V$, $L_{0a}^-\cap L_{0b}^+\cap V$, $L_{0a}^-\cap L_{0b}^-\cap V$ are all nonempty.

Usually, there will be a discrete set of points $S = \left\{{x_i}\right\}_{i\in I}$ in X which will be of interest. By discrete we mean that any compact subset of X contains finitely many points of S. Note that if $${ \liminf_{a,b\in S} d(a,b) > 0 }$$, then S is discrete.

Definition 2.5   We say a proper, path connected metric space X is Brillouin if it satisfies the following conditions:

1:

X is metrically consistent.

2:

For all a, b in X, the mediatrices L_ab are minimally separating sets.

3:

For any three distinct points 0, a, and b in X, the mediatrices L_0a and L_0b are topologically transversal.

The last two conditions in the above definition may be weakened to apply only to those mediatrices L_ab where a and b in S. In this case, we will say that X is Brillouin over S, if it is not obvious from the context.

      

Figure: set L_(0,0),(a,a) contains two quarter-planes.
Figure: L_(0,0),(4,6) (thin solid line) and L_(0,0),(2,4) (thick grey line) are not transverse.
Figure: The mediatrices L_0a for $\mbox{$\Bbb R$ }^2$ with the Manhattan metric and a in the lattice $\left \{{(m,n\sqrt {2})}\right \}$.

Example 2.6    Equip $\mbox{$\Bbb R$ }^2$ with the ``Manhattan metric'', that is, d(p,q) = |p₁ - q₁| + |p₂ - q₂|. In this metric, a circle C_r(p)is a diamond of side length $r\sqrt{2}$ centered at p, so condition 1 is satisfied. However, condition 2 fails: if the coordinates of a point a are equal, then L_0a consists of a line segment and two quarter-planes (see Fig. 2.1). If the discrete set Scontains no such points, we can still run into trouble with topological transversality. For example, the mediatrices L_(0,0),(2,4) and L_(0,0),(4,6) both contain the ray $\left\{{(t,1) \,\,\vrule{}\,\,t \ge 4}\right\}$(Fig. 2.2). But, if we are careful, we can ensure that the space is Brillouin over S. To achieve this, we must have that for all pairs (a₁,a₂) and (b₁,b₂) in S, $a_1 - a_2 \ne b_1 - b_2$. For example, take S to be an irrational lattice such as $\left\{{(m,n\sqrt{2}) \,\,\vrule{}\,\,m,n \in \mbox{$\Bbb Z$ }}\right\}$. It is easy to check that for all $0,a,b \in S$, the properties of definition 2.5 are true. (From this example, we see that to do well in Manhattan, one should be carefully irrational.)

As mentioned in the introduction, for each $x_0\in S$, the mediatrices L_{x0 a} give a partition of X. Informally, those elements of the partition which are reached by crossing n-1 mediatrices from x₀ form the n-th Brillouin zone, B_n(x₀). This definition is impractical, in part because a path may cross several mediatrices simultaneously, or the same mediatrix more than once. Instead, we will use a definition given in terms of the number of elements of S which are nearest to x. This definition is equivalent to the informal one when X is Brillouin over S (see Prop. 2.13 below). We use the notation $\char93 (S)$ to denote the cardinality of the set S.

  

Figure: we illustrate the definition of the sets b_n(x₀) and B_n(x₀) for the lattice $\mbox{$\Bbb Z$ }^2$ in $\mbox{$\Bbb R$ }^2$. In both pictures, the circle $${C_{d(x,x_0)}(x)}$$ is drawn, and the basepoint x₀ lies in the center of the square at the lower left. On the left side, the point x (marked by a small cross) lies in b₅, and $\char93 \left ( N_r(x) \cap S \right ) = 4$, while x₀ is the only point of S on the circle. On the right, we have m=4 and $\ell =8$, so x lies in all of the sets $B_5, B_6, \ldots, B_{12}$.

Definition 2.7   Let $x\in X$, let n be a positive integer, $n \le \char93 (S)$, and let r=d(x,x₀). Then define the sets b_n(x₀) and B_n(x₀) as follows.

• $x \in b_n(x_0) \iff \char93 \left( N_r(x) \cap S \right) = n-1$     and      $C_r(x) \cap S = \left\{{x_0}\right\}$.
• $x \in B_n(x_0) \iff \char93 \left( N_r(x) \cap S \right) = m$     and      $\char93 \left( C_r(x) \cap S \right) = \ell$,     where $l,m \in \mbox{$\Bbb Z$ }^+$

Here the point x₀ is called the base point, and the set B_n(x₀)is the n-th Brillouin zone with base point x₀. Note that in the second part, if m=n-1 and $\ell=1$, then $x \in b_n(x_0)$. So $b_n(x_0) \subseteq B_n(x_0)$. Note also that the complement of b_n(x₀) in B_n(x₀) consists of subsets of mediatrices (see Def. 1.1). Note also that b_n(x₀) is open and that B_n(x₀) is closed. Finally, observe that for fixed x₀ the sets b_n(x₀) are disjoint, but the sets B_n(x₀) are not. In what follows it will be proved that $\left\{{B_n(x_0)}\right\}_{n>0}$cover the space X. Thus we can assign to each point x its Brillouin index as the the largest n for which $x\in B_n(x_0)$. This definition was first given in [Pe1].

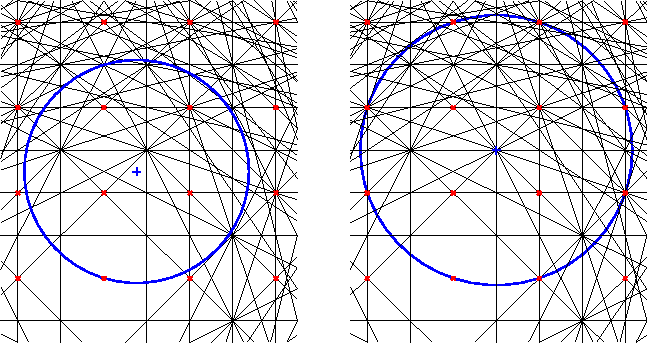The following lemma, which follows immediately from Def. 2.7, explains a basic feature of the zones, namely that they are concentric in in a weak sense. This property is also apparent from the figures.

Lemma 2.8   Any continuous path from x₀ to B_n(x₀) intersects B_n-1(x₀).

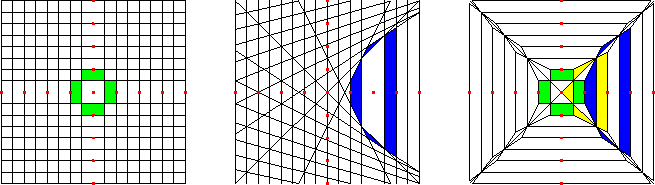
The Brillouin zones actually form a covering of X by non-overlapping closed sets in various ways. This is proved in parts. The next two results assert that the zones B cover X, but the zones b do not. The first of these is an immediate consequence of the definitions. The second is more surprising and leads to corollary 3.4. The fact that the B_i(x_n) is the closure of b_i(x_n) (and thus that the interiors do not overlap) is proved in proposition 2.12. We will use the word ``tiling'' for a covering by non-overlapping closed sets.

Lemma 2.9   For fixed n the Brillouin zones tile X in the following sense:

$$\bigcup_i B_i(x_n) = X \quad\;\;{\rm and }\;\;\quad b_i(x_n) \cap b_j(x_n) = \emptyset \quad \;\mbox{if}\; i\neq j.$$

  

Figure: example illustrates Lemma 2.9 and Thm. 2.10. Let S be the discrete set $\left\{{(m,0)}\right\}\cup \left\{{(0,n)}\right\}, m,n\in\mbox{$\Bbb Z$ }$ in the Euclidean plane. On the left is the tiling given by B_i(0,0) and in the middle is the tiling by B_i(2,0). In both cases, b₂ is shaded. On the right is the tiling given by B₂(x_i) as in Thm. 2.10. The sets b₂(0,0), b₂(1,0), and b₂(2,0) have been shaded. Note that this S does not correspond to a group, nor does it satisfy the hypotheses of Prop. 2.11, because there are no isometries which permute S and do not fix the origin.

Theorem 2.10   Let X be a proper, path connected metric space let $S = \left\{{x_i}\right\}_{i\in I}$be a discrete set. Then, for fixed $n \le \char93 (S)$, the sets $\left\{{B_{n_0}(x_i)}\right\}_{i\in I}$ tile X in the following sense:

$$\bigcup_i B_{n}(x_i) = X \quad\;\;{\rm and }\;\;\quad b_{n}(x_i) \cap b_{n}(x_j) = \emptyset \quad\;\mbox{if}\; i\neq j.$$

Proof: First, we show that for any fixed n>0 and each $x\in X$, there is an $x_i \in S$ with $x \in B_{n}(x_i)$. Re-index S so that if $S =\left\{{x_1, x_2, x_3,\ldots }\right\}$ and i < j, then $d(x,x_i) \le d(x,x_j)$. This can be done; since S is a discrete subset and closed balls D_c(x_i) are compact, the subsets of S with $d(x,x_i) \leq c$ are all finite. Let r_i = d(x,x_i). We will show that $x \in B_{n}(x_{n})$.

Note that $r_{n} \geq r_{n-1}$. Suppose first that r_n > r_n-1, then $N_{r_{n}}(x) \cap S$contains exactly n-1 points, and $x_{n} \in C_{r_{n}}(x) \cap S$. Thus $x \in B_{n}(x_{n})$. Note that if r_n+1 > r_n, then we would have $x \in b_{n}(x_{n}) \subset B_{n}(x_{n})$.

If, on the other hand, r_n = r_n-1, then there is a k>0 so that $r_{n} = r_{n-1} = \ldots = r_{n-k}$, and so $\char93 \left( N_{r_{n}}(x) \cap S \right) = {n} -k-1 \leq {n}-1$. But then $\char93 \left(C_{r_{n}}(x)\cap S\right) \ge k+1$, and hence $x \in B_{n}(x_{n})$ as desired.

For the second part, we show that $b_{n}(x_i)\cap b_{n}(x_j) = \emptyset$. If not, then there is a point x in their intersection. If r_i = r_j, then x_i = x_j, because by the definition of b_n(x_k), $\left\{{x_k}\right\} = C_{r_k}(x) \cap S$. If not, then r_i < r_j. In this case, $x_i \in D_{r_i}(x) \subset N_{r_j}(x)$ . Thus, since $\char93 \left( N_{r_i}(x)\cap S \right) = n-1$, N_rj(x) must contain at least n points of S, a contradiction. $\Box$