Introduction

In solid-state physics, the notion of Brillouin zones is used to describe quantum mechanical properties of a crystal. In a crystal, the atoms are arranged in a lattice; for example, in NaCl, the sodium and chorine atoms are arranged along the points of the simple cubic lattice $\mbox{$\Bbb Z$ }^3$. If we pick a specific atom and call it the origin, its first Brillouin zone consists of the points in $\mbox{$\Bbb R$ }^3$ which are closer to the origin than to any other element of the lattice. This same zone can be constructed as follows: for each element a in the lattice, let L_0a be the perpendicular bisecting plane of the line between 0 and a (this plane is called a Bragg plane). The volume about the origin enclosed by these intersecting planes is the first Brillouin zone, b₁(0). This construction also allows us to define the higher Brillouin zones as well: a point x is in b_n if the line connecting it to the origin crosses exactly n-1 planes L_0a, counted with multiplicity.

 

Figure: On the right are the Brillouin zones for the lattice $\mbox{$\Bbb Z$ }^2$ in $\mbox{$\Bbb R$ }^2$. On the left is the outer boundary of the third Brillouin zone for the lattice $\mbox{$\Bbb Z$ }^3$ in $\mbox{$\Bbb R$ }^3$.

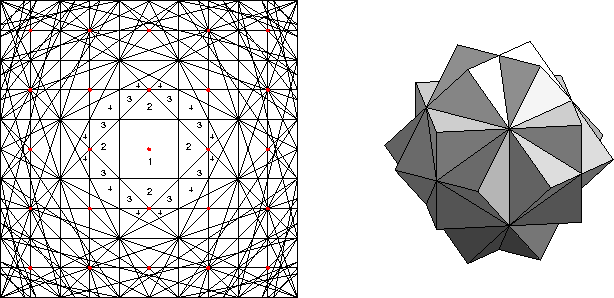This notion was introduced by Brillouin in the 1930s ([Br]), and plays an important role in solid-state theory (see, for example, [AM], or [Jo2], also [Ti]). The construction which gives rise to Brillouin zones is not limited to consideration of crystals, however. For example, in computational geometry, the notion of the Voronoi cell corresponds exactly to the first Brillouin zone described above (see [PS]). We shall also see below how, after suitable generalization, this construction coincides with the Dirichlet domain of Riemannian geometry, and in many cases, to the focal decomposition introduced in [Pe1] (see also [Pe3]).

With some slight hypotheses (see section 2), we generalize the construction of Brillouin zones to any discrete set S in a path-connected, proper metric space X. We generalize the Bragg planes above as mediatrices, defined here.

Definition 1.1   For a and b distinct points in S, define the mediatrix (also called the equidistant set or bisector) L_ab of a and b as:

$$L_{ab} = \left\{{x\in X \,\,\vrule{}\,\,d(x,a) = d(x,b)}\right\} .$$

Now choose a preferred point x₀ in S, and consider the collection of mediatrices $\left\{{L_{x_0,s}}\right\}_{s\in S}$. These partition X into Brillouin zones as above: roughly, the n-th Brillouin zone B_n(x₀) consists of those points in X which are accessible from x₀ by crossing exactly n-1mediatrices. (There is some difficulty accounting for multiple crossings-- see definition 2.7 for a precise statement.)

One basic property of the zones B_n is that they tile the space X:

$$\bigcup_{x_i \in S} B_n(x_i)= X \quad\;\;{\rm and }\;\;\quad B_n(x_0)\cap B_n(x_1) \;\mbox{is small}\;.$$

Here, with some extra hypotheses, ``small'' means of measure zero. Furthermore, again with some extra hypothesis, each zone B<sub>n</sub> has the same area. (This property was ``obvious'' to Brillouin). Both results were proved by Bieberbach in [Bi] in the case of a lattice in $\mbox{$\Bbb R$ }^2$. Indeed, he proves (as we do) that each zone forms a fundamental set for the group action of the lattice. His arguments rely heavily on planar Euclidean geometry, although he remarks that his considerations work equally well in $\mbox{$\Bbb R$ }^d$ and can be extended to ``groups of motions in non-Euclidean spaces''. In [Jo1], Jones proves these results for lattices in $\mbox{$\Bbb R$ }^d$, as well as giving asymptotics for both the distance from B_n to the basepoint, and for the number of connected components of the interior of B_n. In section 2, we show that the tiling result holds for arbitrary discrete sets in a metric space. If the discrete set is generated by a group of isometries, we show that each B_n forms a fundamental set, and consequently all have the same area (see Prop. 2.11).

We now discuss the relationship of Brillouin zones and focal decomposition of Riemannian manifolds.

If x₁(t) and x₂(t) are two solutions of a second order differential equation with x₁(0) = x₂(0) and there is some $T\ne 0$ so that x₁(T) = x₂(T), then the trajectories x₁ and x₂ are said to focus at time T. One can ask how the number of trajectories which focus varies with the endpoint x(T)-- this gives rise to the concept of a focal decomposition (originally called a sigma decomposition). This concept was introduced in [Pe1] and has important applications in physics, for example when computing the semiclassical quantization using the Feynman path integral method (see [Pe3]). There is also a connection with the arithmetic of positive definite quadratic forms (see [Pe2], [KP], and [Pe3]). Brillouin zones have a similar connection with arithmetic, as can be seen in section 4.

More specifically, consider the two-point boundary problem

$$\ddot{x} = f(t,x,\dot{x}), \qquad x(t_0)=x_0, \qquad x(t_1)=x_1, \qquad x, t, \dot{x}, \ddot{x} \in \mbox{$\Bbb R$}.$$

Associated with this equation, there is a partition of $\mbox{$\Bbb R$ }^4$ into sets $\Sigma_{k}$, where (x₀,x₁,t₀,t₁) is in $\Sigma_{k}$if there are exactly k solutions which connect (x₀,t₀) to (x₁,t₁). This partition is the focal decomposition with respect to the boundary value problem. In [PT], several explicit examples are worked out, in particular the fundamental example of the pendulum $\ddot{x} = -\sin x$. Also, using results of Hironaka ([Hi]) and Hardt ([Ha]), the possibility of a general, analytic theory was pointed out. In particular, under very general hypotheses, the focal decomposition yields an analytic Whitney stratification.

Later, in [KP], the idea of focal decomposition was approached in the context of geodesics of a Riemannian manifold M (in addition to a reformulation of the main theorem of [PT]). Here, one takes a basepoint x₀ in the manifold M: two geodesics $\gamma_1$ and $\gamma_2$focus at some point $y\in M$ if $\gamma_1(T) = y = \gamma_2(T)$. This gives rise to a decomposition of the tangent space of M at x into regions where the same number of geodesics focus.

In order to study focusing of geodesics on an orbifold (M,g) with metric g via Brillouin zones, we do the following. Choose a base-point p₀ in M and construct the universal cover X, lifting p₀ to a point x₀ in X. Let $\gamma$ be a smooth curve in M with initial point p₀ and endpoint p. Lift $\gamma$ to ${\tilde \gamma}$ in X with initial point x₀. Its endpoint will be some $x \in \pi^{-1}(p)$. The metric g on M is lifted to a metric ${\tilde g}$ on X by setting ${\tilde g} = \pi^* g$. Under the above conditions, the group G of deck transformations is discontinuous and so $\pi^{-1}(p_0)\subset X$ is a discrete set. One can ask how many geodesics of length t there are which start at p₀end in p, or translated to $(X,{\tilde \gamma})$, this becomes: How many mediatrices L_x0,s intersect at x, as s ranges over $\pi^{-1}(p_0)$?

Notice that if the universal cover of M coincides with the tangent space TM_x, the focal decomposition of [KP] and that given by Brillouin zones will be the same. If the universal cover and the tangent space are homeomorphic (as is the case for a manifold of constant negative curvature), the two decompositions are not identical, but there is a clear correspondence. However, if the universal cover of the manifold is not homeomorphic to the tangent space at the base point, the focal decomposition and that given by constructing Brillouin zones in the universal cover are completely different. For example, let M be $\mbox{$\Bbb S$ }^n$, and let x be any point in it. The focal decomposition with respect to x gives a collection of nested n-1-spheres centered at x; on each of these infinitely many geodesics focus (each sphere is mapped by the exponential to either x or its antipodal point). Between the spheres are bands in which no focusing occurs. (See [Pe3]). However, using the construction outlined in the previous paragraph gives a very different result. Since $\mbox{$\Bbb S$ }^n$ is simply connected, it is its own universal cover. There is only one point in our discrete set, and so the entire sphere Sⁿ is in the first zone B₁.

The organization of this paper is as follows. In section 2, we set up the general machinery we need, and prove the main theorems in the context of a discrete set S in a proper metric space.

Section 3 explores this in the context of manifolds of constant curvature. The universal cover is $\mbox{$\Bbb R$ }^n$, $\mbox{$\Bbb S$ }^n$, or $\mbox{$\Bbb H$ }^n$, and the group G of deck transformations is a discrete group of isometries (see [doC]). The discrete set S is the orbit of a point not fixed by any element of G under this discontinuous group. It is easy to see that the mediatrices in this case are totally geodesic spaces. From the basic property explained above, one can deduce that the n-th Brillouin zone is a fundamental domain for the group G in X.

In section 4, we calculate exactly the number of geodesics of length t that connect the origin to itself in two cases: the flat torus $\mbox{$\Bbb R$ }^2/\mbox{$\Bbb Z$ }^2$ and the Riemann surfaces $\mbox{$\Bbb H$ }^2/\Gamma(p)$, for $p \in \left\{{2,3,5}\right\}$. While these calculations could, of course, be done independent of our construction, the Brillouin zones help visualize the process.

In the final section, we give a nontrivial example in the case of a non-Riemannian metric, and mention a connection to the question of how many integer solutions there are to the equation a^k + b^k = n, for fixed k.

Acknowledgments: It is a pleasure to acknowledge useful conversations with Federico Bonetto, Johann Dupont, Bernie Maskit, John Milnor, Chi-Han Sah, and Duncan Sands.