

Next: Non-Riemannian examples
Up: ON BRILLOUIN ZONES
Previous: Brillouin zones in spaces
Focusing in two Riemannian examples
In this section, we give two examples (one of them new as far as we know)
of focusing. Suppose that at t=0 geodesics start emanating in all possible
directions from the origin. At certain times
t1, t2, ...., we will
see geodesics returning to the origin. We derive expressions for the number
of geodesics returning at tn in two cases. First, as introductory example
we will discuss this for
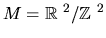 (a more complete discussion of this
example can be found in [Pe3]). Second, we will deal with a much more
unusual example, namely
(a more complete discussion of this
example can be found in [Pe3]). Second, we will deal with a much more
unusual example, namely
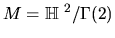 ,
where
,
where 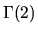 is a
subgroup of
is a
subgroup of
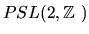 called the principal congruence subgroup of
level 2 (defined in more detail below). We note that it seems to be
considerably harder to count geodesics that focus in points other than
the origin.
Before continuing, consider the classical problem of counting
Rg(n), the number of solutions in
called the principal congruence subgroup of
level 2 (defined in more detail below). We note that it seems to be
considerably harder to count geodesics that focus in points other than
the origin.
Before continuing, consider the classical problem of counting
Rg(n), the number of solutions in
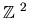 of
of
p2 + q2 = n .
Let
be the prime decomposition of the number n, where
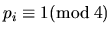 and
and
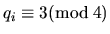 .
The following classical result of Gauss (see
[NZM]) will be very useful.
.
The following classical result of Gauss (see
[NZM]) will be very useful.
Lemma 4.1
Rg(
n)
is zero whenever n is not an integer, or any of the 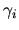 is
odd. Otherwise,
is
odd. Otherwise,
Example 4.2
Choose an origin in
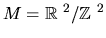
and lift it to the
origin in
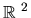
.
We have that
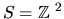
.
Let
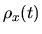
be the number
of geodesics of length
t that connect the origin to the point
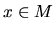
.
Proposition 4.3
In the flat torus, the number of geodesics of length
t that connect the
the origin to itself is given by
Proof: Notice that by definition geodesics of length t leaving from
the origin in
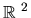 reach the points contained in Ct(0). Only if t2is an integer does this circle intersect points in
reach the points contained in Ct(0). Only if t2is an integer does this circle intersect points in
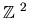 .
.
Example 4.4
We now turn to the next example. Recall that
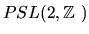
can be identified with the group of two by two matrices with integer entries
and determinant one, and with multiplication by -1 as equivalence.
The group
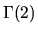
is an
order 3 subgroup of
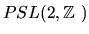
obtained as the quotient of
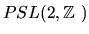
by the order 3 subgroup generated by
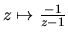
.
This group has important applications in number theory. The action of
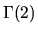
on
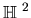
is given by the Möbius transformations
where
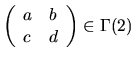
.
We need a well-known result, which we reproduce here for completeness.
Lemma 4.5
The orbit
S of 0
in
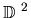 under the fundamental group of
under the fundamental group of
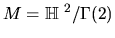 is
is
Figure:
The orbit of 0 under 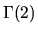 in the hyperbolic
disk, and the corresponding Brillouin zones.
in the hyperbolic
disk, and the corresponding Brillouin zones.
 |
Proof: Following the conventions in [Be], define
Push back the transformation
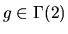
from
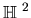
to
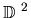
by
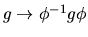
to obtain a representation of
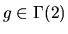
as a transformation in
SU(1,1) acting on
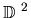
.
The matrix
representation of this transformation is given by:
where
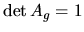
,
since this matrix is conjugated to
g, whose determinant is equal to 1. Let
and
Ag now written as
Here the numbers
p,
q,
r,
s are in
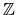
and must satisfy the following parity conditions:
Recall that the determinant of
Ag is equal to 1, therefore
p2+q2+1=r2+s2.
It is easy to see that this last equation together with any one of the above parity conditions, say the one satisfied by
p and
r (
q and
s), imply the parity relation on
q and
s (
p and
r). This proves our claim.
Minor modifications to this argument give exact
counts on the number of geodesics of length t which connect the origin to
itself for
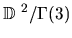 and
and
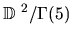 .
We shall do this now.
Let
.
We shall do this now.
Let
Transporting this group to
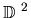 as before, we obtain the representation
as before, we obtain the representation
Theorem 4.8
The number of geodesics of length t which connect the origin to itself in
the surfaces
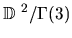 and
and
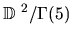 are given by
respectively.
are given by
respectively.
Proof: First, let us consider N=3. Since N is odd, the congruence conditions on
r,p,s, and q imply that
Note that the equation
is satisfied exactly
Rg(n/32) times. (Recall that if n/9 is not an
integer,
Rg(n/9) = 0.)
For fixed n, let (p,q) be any one of the solutions. We need to decide
how many solutions the equation
admits. The solution of the first equation implies that 3 divides n.
Thus
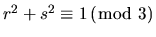 .
Consequently, there are 4 choices
.
Consequently, there are 4 choices 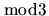 for the pair (r,s), namely
(0,1), (1,0), (0,2), and (2,0).
for the pair (r,s), namely
(0,1), (1,0), (0,2), and (2,0).
Let
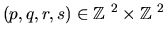 be any solution to
n=p2+q2 = r2 + s2 -1 with
be any solution to
n=p2+q2 = r2 + s2 -1 with
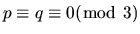 .
For each choice of (p,q), we have exactly Rg(n+1) choices of (r,s).
Now let R denote the product of the rotations by
.
For each choice of (p,q), we have exactly Rg(n+1) choices of (r,s).
Now let R denote the product of the rotations by 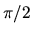 on each of the
components of
on each of the
components of
 .
Using Lemma 4.6, we see that
all such solutions can be obtained from just one by applying R repeatedly.
It is easy to check that each quadruple of solutions thus constructed runs
exactly once through the above list. Since precisely one out of the four
associated solutions is compatible with the conditions,
the total number of solutions is exactly:
.
Using Lemma 4.6, we see that
all such solutions can be obtained from just one by applying R repeatedly.
It is easy to check that each quadruple of solutions thus constructed runs
exactly once through the above list. Since precisely one out of the four
associated solutions is compatible with the conditions,
the total number of solutions is exactly:
Using the relationship between the Euclidean distance and the Poincaré
length as before gives the result.
For N=5, the proof can be literally transcribed to obtain the second result.


Next: Non-Riemannian examples
Up: ON BRILLOUIN ZONES
Previous: Brillouin zones in spaces
Translated from LaTeX by Scott Sutherland
1998-06-12
![]() (a more complete discussion of this
example can be found in [Pe3]). Second, we will deal with a much more
unusual example, namely
(a more complete discussion of this
example can be found in [Pe3]). Second, we will deal with a much more
unusual example, namely
![]() ,
where
,
where ![]() is a
subgroup of
is a
subgroup of
![]() called the principal congruence subgroup of
level 2 (defined in more detail below). We note that it seems to be
considerably harder to count geodesics that focus in points other than
the origin.
Before continuing, consider the classical problem of counting
Rg(n), the number of solutions in
called the principal congruence subgroup of
level 2 (defined in more detail below). We note that it seems to be
considerably harder to count geodesics that focus in points other than
the origin.
Before continuing, consider the classical problem of counting
Rg(n), the number of solutions in
![]() of
of
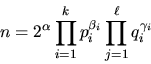
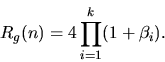
![]() reach the points contained in Ct(0). Only if t2is an integer does this circle intersect points in
reach the points contained in Ct(0). Only if t2is an integer does this circle intersect points in
![]() .
.
![]()
 .
We need a well-known result, which we reproduce here for completeness.
.
We need a well-known result, which we reproduce here for completeness.

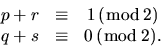
![]() and
and
![]() .
We shall do this now.
Let
.
We shall do this now.
Let
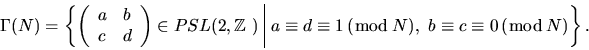
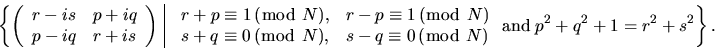
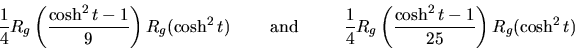
![]() be any solution to
n=p2+q2 = r2 + s2 -1 with
be any solution to
n=p2+q2 = r2 + s2 -1 with
![]() .
For each choice of (p,q), we have exactly Rg(n+1) choices of (r,s).
Now let R denote the product of the rotations by
.
For each choice of (p,q), we have exactly Rg(n+1) choices of (r,s).
Now let R denote the product of the rotations by ![]() on each of the
components of
on each of the
components of
![]() .
Using Lemma 4.6, we see that
all such solutions can be obtained from just one by applying R repeatedly.
It is easy to check that each quadruple of solutions thus constructed runs
exactly once through the above list. Since precisely one out of the four
associated solutions is compatible with the conditions,
the total number of solutions is exactly:
.
Using Lemma 4.6, we see that
all such solutions can be obtained from just one by applying R repeatedly.
It is easy to check that each quadruple of solutions thus constructed runs
exactly once through the above list. Since precisely one out of the four
associated solutions is compatible with the conditions,
the total number of solutions is exactly:
![]()