
The (one-dimensional) wave equation is the partial differential equation
In general any function f(x+ ct) or f(x- ct) satisfies this equation.
If we plot f(x+ ct) as a function of x for various values of t,
the graph moves to the left with speed c as t varies. It can be
thought of as a wave moving along the medium (string or column).
Similarly f(x- ct)moves to the right. Hence the "wave equation"
and the interpretation of c as velocity.
The wave equation has vibration-type solutions when it is
supplemented by boundary conditions. There are two types
that will interest us (to lighten the notation, we will consider a string or
a pipe of length ![]() ,
and in the
air-column cases, u(x, t) will be the difference between the pressure
at (x, t) and the outside pressure):
,
and in the
air-column cases, u(x, t) will be the difference between the pressure
at (x, t) and the outside pressure):
|
I. u = 0 at both ends, for all values of t. This
corresponds to a string with both ends fixed,
or a pipe open at both ends.
In this case, the functions
|
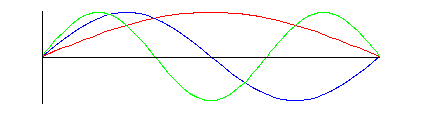 Solutions to the wave equation for the closed string or the open pipe, shown as functions of x when t = 0. Red: n = 1; blue: n = 2; green: n = 3. |
II. u = 0 at one end, and
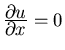 at
the other. This corresponds to pipe open at
the end where u = 0 and closed at the other.
at
the other. This corresponds to pipe open at
the end where u = 0 and closed at the other.
In case II, the functions
|
 Solutions to the wave equation for the half-open pipe, shown as functions of x when t = 0. Red: n = 1/2; blue: n = 3/2; green: n = 5/2. |
For a pipe or string of length L, a factor of ![]() must be inserted before
each of the x and t arguments.
must be inserted before
each of the x and t arguments.
Frequency. The pitch of the sound produced by the vibrations
depends on the frequency, which can be determined from the
time-dependent factor
![]() .
For vibrating
columns of air, the c in question is the speed of sound,
344 m/sec at sea level. The frequency of the
sound corresponding to the nth harmonic is then
.
For vibrating
columns of air, the c in question is the speed of sound,
344 m/sec at sea level. The frequency of the
sound corresponding to the nth harmonic is then
![]() for the open pipe and
for the open pipe and
![]() for the half-open one,
which gives
344/2L
Hz and
344/4L
Hz as
fundamental (lowest) frequencies for
the open pipe and the half-open pipe respectively.
for the half-open one,
which gives
344/2L
Hz and
344/4L
Hz as
fundamental (lowest) frequencies for
the open pipe and the half-open pipe respectively.
In our Song Sparrow record
the lowest frequency shown is the "D" at 2325 Hz. This would
correspond to an open pipe of length L= 7.1 cm, or a half-open
pipe of length 3.7cm, kind of a stretch given
the bird's length of some 15cm including the tail. The presence of the
second harmonic would correspond to the "pipe" being slightly
open at the closed end: an open pipe has fundamental frequency twice
that of the half-open pipe of the same length. The standard reference
for these problems is Crawford H. Greenewalt, Bird Song: Acoustics and
Physiology, Smithsonian Institution Press, Washington 1968.
The Mourning Dove Zenaida macrocoura, common in North America, measures 30cm including a long tail but has a coo at 445 Hz, corresponding to a half-open pipe of length 19.3cm. Where could a vocal organ of that size fit in a bird so small? Eppure canta.