piano3

$e-MATH$
The mathematics of piano tuning

3. The equal-tempered keyboard

The interval from a note to the note of twice the frequency is called an octave, while the interval to the note of 3/2 the frequency is called a perfect fifth. These are the most natural intervals in music. But for a piano to be able to play down an octave and up perfect fifth for each of its notes would require an infinite number of keys. The compromise solution in common use since the middle of the nineteenth century is equal temperament. It is based on a rational approximation to log₂3. The continued fraction approximation of frac(log₂3) yields 1/2, 3/5, 7/12, 24/41, ... as best rational approximations. The one to take is 7/12.

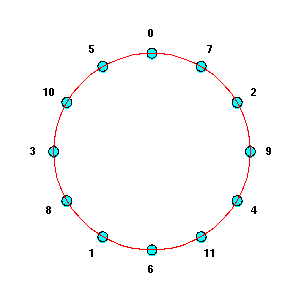With 7/12 as approximation to frac(log₂3), iterating the "third harmonic" construction yields exactly twelve pitch classes.

If "0" corresponded to C on a piano, then the pitch classes would run as follows:

0	1	2	3	4	5	6	7	8	9	10	11
C	G	D	A	E	B	F#	C#	G#	D#	A#	F

Since the interval from each note to the next is a (not quite perfect) fifth, this sequence of pitch classes is referred to as "the circle of fifths."

The beauty of equal tempering is that the whole arrangement has a rotational symmetry of order 12. A piano piece written with starting pitch C can be "transposed" up so as to start with F by shifting each note five steps clockwise. No new notes are required. All the relationships between the notes of the piece will be the same: it will be the same piece of music, just set higher.

The price paid for this convenience is that none of the intervals, except the octaves, sounds quite right. In the New Grove Dictionary of Music and Musicians there is a 14-page entry for "Temperament" which explains the history of the problem and the pros and cons of the various solutions. In particular it is still not known for sure whether the "well-tempering" consecrated by Bach was equal tempering or not. See also the Grove entry for "Well-tempered clavier." Jim Loy's web-page The Well-Tempered Scale comes down squarely on the "or not" side.