piano2

$e-MATH$
The mathematics of piano tuning

2. Frequencies and notes

The frequency or frequency spectrum of a sound is a physical observable. The way that frequency is interpreted as a note is a phenomenon of physiology, psychology and culture. Without getting into the many fascinating details of this phenomenon, I will just list two incontrovertible (I believe) facts about the perception of musical sound in western cultures.

People judge the distance in pitch ("interval") between two sounds as a function of the ratio of their frequencies.
Two sounds whose frequencies are in the ratio 2:1 are judged as representing the "same" note in different pitches.

These facts have immediate mathematical consequences.

In any analysis of notes, i.e. of the perception of pitch, sounds should be organized according to the logarithms of their frequencies. This is because logarithm functions are characterized (among continuous functions) by the property log(a/b) = log(a) - log(b): the distance between two logarithms depends only on the ratio of their arguments.
In a geometric representation of the set of pitch classes, frequencies that differ by a factor of 2 should correspond to the same point, since they belong to the same pitch class. The simplest way to do this is to use logarithms to the base 2, and to only keep the fractional part of the logarithm. This way if a=2b, log₂a = log₂2 + log₂b = 1+log₂b, so the fractional parts will be the same.

Putting these two points together: a faithful geometric picture of the set of pitch classes is a circle of length 1. The easiest way to place the points on the circle is to choose as basepoint the pitch class correcponding to frequencies which are exact powers of 2, e.g. 256 (approximately middle C), 512, 1024, etc. Then each other pitch class gets displayed along the circle at a distance from the basepoint equal to the fractional part of its logarithm to the base 2. As the frequency approaches twice the base frequency, the fractional part of its logarithm to the base 2 gets closer to 1, and we get back to the basepoint, as required.
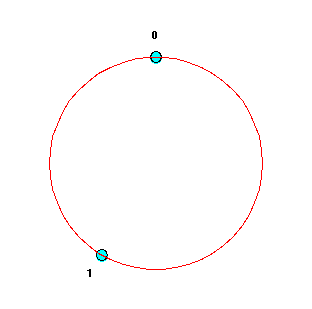
Here is a circle of length 1 with a basepoint marked "0" and the class corresponding to its third harmonic marked "1". The distance between two points along the circle is the fractional part of the logarithm of the ratio of their frequencies; in this case it is the fractional part of log₂3, or frac(log₂3) = 0.584962501.... (The points are drawn here with pitch increasing clockwise).

The pitch class "1" deserves to have its own third harmonic added to the collection; call this new pitch class "2." It will be placed on the circle at distance frac(log₂3)= 0.584962501... clockwise from pitch "1." This process can be repeated to give pitch classes "3," "4," "5," etc. Each of these classes is naturally related to the one before by the same procedure that the Song Sparrow uses in moving from D to A. Because log₂(3) is irrational, these classes are all different.