7. Why is the regular hexagon special?
So now we look at one of the regions of type II. We will show
that the ratio of the area inside the disc to that of the whole type II region
is at most equal to the ratio in the special case when the central
angle is 60o.
This can be done by an explicit calculation,
and the claim then reduces to the observation that
the function sin(x) / x is monotonic decreasing
in the range between 0 and 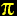 /2.
/2.
But it can also be demonstrated by a purely
geometric argument.
The figure on the left above shows
the special case. In the figure on the right
the animation generates the other cases.
As the central angle decreases we also generate the image
of the left disc
under the unique
linear transformation which acts by scaling vertically
and horizontally, transforming
the original
(60o) triangle to the narrower isosceles one.
This is indicated in the figure above.
Linear transformations preserve ratios of areas.
The animation then shows how
the largest ratio of circular sector to triangle ocurs in a type II sector
when
the central angle is 60o.
In summary, the
density will achieve the maximum possible only when there are no
regions of the first or third type and when the central
angle of each of the regions of type II is exactly
60o.
These criteria uniquely determine the cells in
a hexagonal packing.
The same proof explains the argument about the 6 discs
surrounding a single one, since it shows that the hexagon
circumscribing a disc is the Voronoi cell of smallest
area containing it.
The analogous argument fails in 3D, since the smallest cell
surrounding a sphere is known to be a regular dodecahedron,
a shape which cannot partition all of space.
In particular, as Kepler himself well knew and well described,
this is not the same as the cell
in the densest layout of spheres
throughout all of space. It is this disparity
between local and global behaviour that
offers a serious obstacle to a simple proof
of Kepler's conjecture in 3D.

