There are a few characteristic properties of Voronoi cells that we shall require.

(1) Since all the discs are of equal size, a disc is contained within its Voronoi cell.

(2) If P and Q are two points in the plane, then the set of points closer to P than to Q is the half-plane containing P and bounded by the line half-way between them. In any configuration, therefore, the Voronoi cell of a disc is the intersection of all the half-planes determined in this way by that disc and other discs in the collection. It follows that every Voronoi cell is convex.

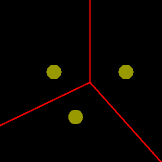
(3) For a layout of three discs, the Voronoi cells will be simplicial cones with a common vertex at one point - the triple point - which is the common intersection of all three bisectors between the points - except in the singular case when the bisectors are mutually parallel. This triple point will be equi-distant from each of the three discs. Draw from the triple point the pair of tangent line segments to each of the discs, making a kind of dunce's cap. The vertex angle of that cap will be the same for each disc, since this angle depends only on distance of the triple point from the disc. Because Voronoi cells are convex, the whole of each cap will be contained in a the Voronoi cell of its disc.

If two discs are close enough, then there will be a `dead' region (shown in pink in the animation) on the line half-way between them where the triple point for a third disc cannot be found. Moving the third disc (which is `live') shows how the three vertex angles remain equal, and the caps contained in Voronoi cells.

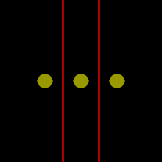
Suppose we fix two of the three discs and ask how this triple point varies as the third disc moves around. If the two discs are far enough apart, the triple point can be anywhere on the line bisecting the given pair. But as soon as they are close enough together, there will be a dead space on this line right in between the two discs where the triple point can never be found. This dead space will exist as soon as the centres of discs are closer than 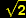times their common diameter. As we decrease the distance between the two discs, the size of the dead region will expand. This is shown in the animation at left, where the dead space is highlighted in pink. The figure also illustrates that the caps drawn from the triple point don't overlap (except possibly along their edges), and that their common vertex angle can be at most one-third of 360o or 120o.