e-MATH

Packing Pennies in the Plane


5. The hexagonally circumscribed circle

The vertex angle of the cap decreases with distance from the disc.
Circumscribe a disc with a regular hexagon, and circumscribe the hexagon with a circle. This gives what I call the hexagonally circumscribed circle of the original disc. It is a concentric circle whose radius is times the original one. If P is any point outside the original disc, the two tangents from P to that disc bound what I call the cap corresponding to P and the disc. The key property we shall need later on is that the vertex angle at P is a decreasing function of the distance of P from the disc. This vertex angle will be exactly 120o precisely when P lies on the hexagonally circumscribed circle, because then it is a vertex of a circumscribed hexagon. So when this angle is less than 120o the point P must lie outside the hexagonally circumscribed circle. This vertex angle will be exactly 120o precisely when P lies on the hexagonally circumscribed circle, and when this angle is less than 120o the point lies outside the hexagonally circumscribed circle.
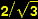
We shall need also another property of these circumscribed circles. Suppose two of them intersect, but that the discs themselves do not intersect. Then that intersection can only intersect the Voronoi cell of a third disc if the three discs are mutually touching in the configuration of discs in a hexagonal packing.

For suppose P to be a point in the intersection of two circumcribed circles, and also in the Voronoi cell of a third disc. The two discs are close enough that the point exactly half-way between them will be in the dead region where the triple point cannot be located. The triple point must therefore lie between P and this half-way point, and also in both hexagonally circumscribed circles. But each of the vertex angles at the capped discs from this triple point must then be at least 120o. This can only happen if this angle is exactly 120o and the three discs are mutually touching.

In the diagram to the right, this means that the points in the yellow rhombus are never in the Voronoi cell of the third disc.

The triple point never lies inside
the hexagonally circumscribed circles.
As a consequence, points in the yellow rhombus
never lie in the Voronoi cell of a third disc.

@2000 American Mathematical Society