

Next: 6 Some Amusements
Up: MAT 200 Course Notes on
Previous: 4 Lengths, areas and
Subsections
A circle  is the set of points at fixed
distance
is the set of points at fixed
distance 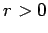 from a given point, its center. The distance
from a given point, its center. The distance 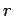 is
called the radius of the circle
is
called the radius of the circle  .
.
The circle  divides the plane into two regions: the inside,
which is the set of points at distance less than
divides the plane into two regions: the inside,
which is the set of points at distance less than 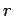 from the center
from the center  ,
and the outside, which consists of all points having distance from
,
and the outside, which consists of all points having distance from  greater than
greater than 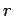 . Note that every line segment from
. Note that every line segment from  to a point on
to a point on
 has the same length
has the same length 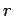 .
.
A line segment from  to a point on
to a point on  is also called a
radius; this should cause no confusion.
is also called a
radius; this should cause no confusion.
A line segment connecting two points of  is called a chord,
if the chord passes through the center, then it is called a
diameter.
is called a chord,
if the chord passes through the center, then it is called a
diameter.
As above, we also use the word diameter to denote the length of a diameter
of  , that is, the number that is twice the radius.
, that is, the number that is twice the radius.
Proposition 5.1
A line  intersects a circle
intersects a circle  in at most two points.
in at most two points.
Proof.
Suppose we had three points,

,

and

, of intersection of

with

.
We first take up the case that  is a diameter. In this case, we would
have at least two of the three points on the same side of
is a diameter. In this case, we would
have at least two of the three points on the same side of  on
on  ; hence
we can suppose that
; hence
we can suppose that  and
and  both lie on the same side of
both lie on the same side of  . However,
by the ruler axiom (Axiom 6), we must have
. However,
by the ruler axiom (Axiom 6), we must have
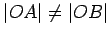 since
since 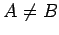 . This contradicts our assumption that
. This contradicts our assumption that  and
and  both lie
on
both lie
on  .
.
We next take up the case that  is not a diameter. We can assume that
is not a diameter. We can assume that  lies between
lies between  and
and  on
on  .
Draw the line segments,
.
Draw the line segments, 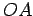 ,
, 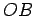 ,
, 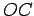 . Then
. Then 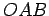 ,
, 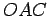 and
and 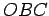 are
triangles. In fact, since
are
triangles. In fact, since
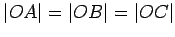 , they are isosceles
triangles. Let
, they are isosceles
triangles. Let 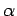 be the measure of the base angles of triangle
be the measure of the base angles of triangle
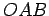 . Then it is also the measure of the base angle of
. Then it is also the measure of the base angle of
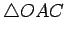 , and
so it is also the measure of the base angle of
, and
so it is also the measure of the base angle of
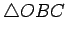 . Since the
two base angles at
. Since the
two base angles at  add up to
add up to 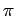 , we obtain that each of the three
triangles have two right angles, which is impossible.
, we obtain that each of the three
triangles have two right angles, which is impossible.

Proposition 5.2
Let  be a chord of a circle
be a chord of a circle  with center
with center  . Then
the perpendicular bisector of
. Then
the perpendicular bisector of  passes through
passes through  .
.
Exercise 5.1
Prove the preceding proposition.
While we have spent a fair amount of time determining when two angles have
the same measure, we have not discussed explicitly calculating the measure
of an angle, except in the case of an angle of measure 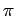 and a right
angle (measure
and a right
angle (measure 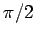 ). We shall do so now.
). We shall do so now.
First, we assume the well-known property that the circumference
(that is, the arc length) of a circle of radius 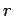 is
is 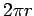 .
.
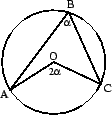
Now let  and
and  be two points on a circle of radius 1 and center
be two points on a circle of radius 1 and center  .
The radii
.
The radii 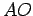 and
and 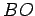 make two angles
make two angles 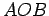 (the
``inner'' and the ``outer'' angles); call them
(the
``inner'' and the ``outer'' angles); call them 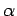 and
and 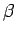 .
An angle such as
.
An angle such as 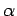 whose vertex is at the center of the circle is
called a central angle. Notice that
whose vertex is at the center of the circle is
called a central angle. Notice that
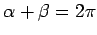 , no
matter where
, no
matter where  and
and  lie on
lie on  .
If
.
If  and
and  are the endpoints of a diameter, they divide the circle into
two arcs, each of length
are the endpoints of a diameter, they divide the circle into
two arcs, each of length 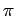 ; note also that the measure of the angles
; note also that the measure of the angles
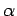 and
and 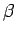 are also
are also 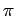 . In other cases, the length of the arc
subtended by the angle
. In other cases, the length of the arc
subtended by the angle 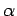 will be whatever fraction of
will be whatever fraction of 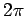 that
that
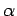 is of the entire circle. For example, if
is of the entire circle. For example, if 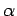 is a right
angle, it will take up
is a right
angle, it will take up 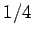 of the circle, and the corresponding arc length
will be
of the circle, and the corresponding arc length
will be 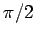 . We define the measure of the angle to be the corresponding
arc length when that angle is the central angle of a circle of radius 1.
. We define the measure of the angle to be the corresponding
arc length when that angle is the central angle of a circle of radius 1.
Proof.
Draw the line
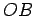
. This divides quadrilateral
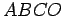
into two isosceles
triangles. Let
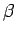
be the measure of the base angles of
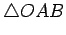
,
and let
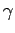
be the measure of the base angles of
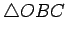
Then
the measure of the requisite central angle is given by

The circle  is circumscribed about
is circumscribed about
 if all
three vertices of the triangle lie on the circle. In this case, we also say
that the triangle is inscribed in the circle.
if all
three vertices of the triangle lie on the circle. In this case, we also say
that the triangle is inscribed in the circle.
Note that another way to describe a circle circumscribed about a triangle is
to say that it is the smallest circle for which every point inside the
triangle is also inside the circle. In this view, the problem of
circumscribing a circle becomes a minimization problem. A given triangle
lies inside many circles, but the circumscribed circle is, in some sense,
the smallest circle which lies outside the given triangle.
It is not immediately obvious that one can always solve this minimization
problem, nor that the solution is unique.
Proposition 5.4 (Uniqueness of Circumscribed Circles)
There is at most one circle
circumscribed about any triangle.
Proof.
Suppose there are two circles

and

which are
circumscribed about

. Since points

,

, and

lie on
both circles,

and

are chords. By
Prop.
5.2, the perpendicular bisectors of

and

both pass through the centers of

and

.
Since these two distinct lines can intersect in at most one point,

and

share the same center

. Since
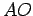
is a radius for both
circles, they have the same center and radius, and hence are the same
circle.

Theorem 5.5 (Existence of Circumscribed Circles)
Given
 , there is always exactly one circle
, there is always exactly one circle  circumscribed about it.
circumscribed about it.
Proof.
We need to show that the perpendicular bisectors of the sides of

meet at a point, and that this point is equidistant from all
three vertices. Then the requisite circle will have this point as its
center

, and the radius will be the length of
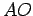
. Uniqueness was shown
in Prop.
5.4.
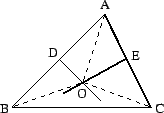
Let  and
and 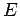 be the midpoints of sides
be the midpoints of sides  and
and  respectively. Draw
the perpendicular bisectors of
respectively. Draw
the perpendicular bisectors of  and
and  , and let
, and let  be the point where
these two lines meet (note that
be the point where
these two lines meet (note that  need not be inside the triangle). Draw
the lines
need not be inside the triangle). Draw
the lines 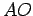 ,
, 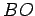 and
and 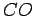 .
.
We cannot have both that
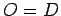
and
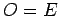
(since
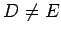
), hence we can
assume without loss of generality that
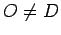
. Then we have
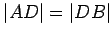
,
angles
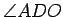
and
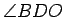
are both right angles, and of course,
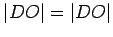
. Hence,
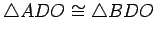
by
SAS. In particular,
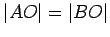
. If
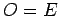
, then we have shown that
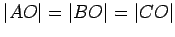
, from which
it follows that there is a circumscribed circle with center

and radius
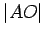
.
If 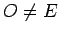 , then we repeat the above argument to show that
, then we repeat the above argument to show that
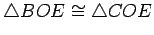 , from which, as above, it follows that
, from which, as above, it follows that
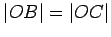 . Again, this shows that there is a circumscribed circle.
. Again, this shows that there is a circumscribed circle.

Corollary 5.6
In any triangle, the three perpendicular bisectors of the sides meet at a
point.
Exercise 5.2
Explain why Theorem 5.5 implies this corollary.
Corollary 5.7 (Three Points Determine a Circle)
Given any three non-colinear points, there is exactly one circle which
passes through all three of them.
Exercise 5.3
Explain why this corollary follows from
Theorem 5.5.
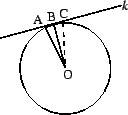
A line that meets a circle in exactly one point is a tangent line
to the circle at the point of intersection. Our first problem is to show
that there is one and only one tangent line at each point of a circle.
Proposition 5.8
Let  be a point on the circle
be a point on the circle  , and let
, and let  be the line through
be the line through
 perpendicular to the radius at
perpendicular to the radius at  . Then
. Then  is tangent to
is tangent to  .
.
Proof.
There are only three possibilities for

: it either is disjoint from

, which cannot be, as

is a common point; or it is tangent to

at

; or it meets

at another point

. If

meets

at

then
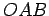
is a triangle, where
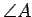
is a right
angle. Since
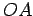
and
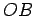
are both radii,
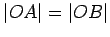
. Hence
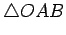
is isosceles. Hence
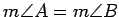
. We have constructed a
triangle with two right angles, which cannot be; i.e., we have reached a
contradiction.

Proposition 5.9
If  is a line tangent to the circle
is a line tangent to the circle  at the point
at the point  , then
, then  is perpendicular to the radius ending at
is perpendicular to the radius ending at  .
.
Proof.
We will prove the contrapositive: if

is a line passing through

,
where

is not perpendicular to the radius, then

is not tangent to

.
Draw the line segment
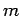
from

to

, where
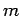
is perpendicular to

. Let

be the point of intersection of

and
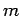
. On

, mark off
the distance
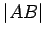
from

to some point

, on the other side of

from

. Since
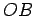
is perpendicular to

,
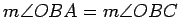
.
By
SAS,
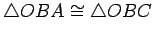
, and so
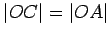
. Thus both

and

lie on

, and

intersects

in two
points. Thus,

is not tangent to

.

Corollary 5.10
Let  be a point on the circle
be a point on the circle  . Then there is exactly
one line through
. Then there is exactly
one line through  tangent to
tangent to  .
.
Exercise 5.4
Prove this Corollary.
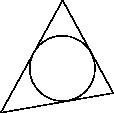
A circle  is inscribed in
is inscribed in
 if all three
sides of the triangle are tangent to
if all three
sides of the triangle are tangent to  . One can view the inscribed
circle as being the largest circle whose interior lies entirely inside the
triangle. (Note that it is not quite correct to say that the circle lies
entirely inside the triangle, because the triangle and the circle share
three points.)
. One can view the inscribed
circle as being the largest circle whose interior lies entirely inside the
triangle. (Note that it is not quite correct to say that the circle lies
entirely inside the triangle, because the triangle and the circle share
three points.)
We start the search for the inscribed circle with the question of what it
means for the circle to have two tangents which are not parallel.
Proposition 5.11
Let  be a point outside the circle
be a point outside the circle  , and let
, and let 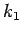 and
and 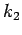 be tangents to
be tangents to  emanating from
emanating from  . Then the line segment
. Then the line segment
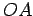 bisects the angle between
bisects the angle between 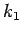 and
and 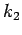 .
.
Proof.
Let
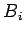
be the point where
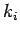
is tangent to

, for
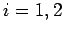
. Draw
the lines
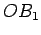
and
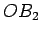
. Observe that
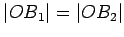
, and that, since
radii are perpendicular to tangents,
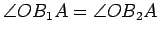
, and these
are both right angles.
By SSA,
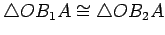 . Hence
. Hence
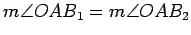 .
.

From the above, we see that if there is an inscribed circle for
 , then its center lies at the point of intersection of the three angle
bisectors, and its radius is the distance from this point to the three
sides. Hence we have proven the following.
, then its center lies at the point of intersection of the three angle
bisectors, and its radius is the distance from this point to the three
sides. Hence we have proven the following.
Corollary 5.12 (Inscribed circles are unique)
Every triangle has at most one inscribed circle.
Theorem 5.13
Every triangle has an inscribed circle.
This theorem gives another proof of the result of
exercise 2.16.
Corollary 5.14
The three angle bisectors of a triangle meet at a point; this point is the
center of the inscribed circle.
Exercise 5.5
Give a proof of this corollary using the above theorem.
Exercise 5.6
Let
 and
and
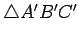 be
such that
be
such that
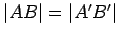 ,
,
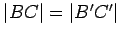 , and
, and
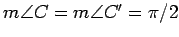 . Prove that
. Prove that
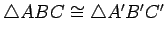 .
.
Exercise 5.7
Let  and
and  be points on the circle
be points on the circle  . Let
. Let  be the line
tangent to
be the line
tangent to  at
at  and let
and let 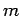 be the line tangent to
be the line tangent to  at
at
 . Prove that if
. Prove that if  and
and  are parallel, then the line segment
are parallel, then the line segment  is a
diameter of
is a
diameter of  .
.


Next: 6 Some Amusements
Up: MAT 200 Course Notes on
Previous: 4 Lengths, areas and
Scott Sutherland
2002-12-18
![]() divides the plane into two regions: the inside,
which is the set of points at distance less than
divides the plane into two regions: the inside,
which is the set of points at distance less than ![]() from the center
from the center ![]() ,
and the outside, which consists of all points having distance from
,
and the outside, which consists of all points having distance from ![]() greater than
greater than ![]() . Note that every line segment from
. Note that every line segment from ![]() to a point on
to a point on
![]() has the same length
has the same length ![]() .
.
![]() to a point on
to a point on ![]() is also called a
radius; this should cause no confusion.
is also called a
radius; this should cause no confusion.
![]() is called a chord,
if the chord passes through the center, then it is called a
diameter.
is called a chord,
if the chord passes through the center, then it is called a
diameter.
![]() , that is, the number that is twice the radius.
, that is, the number that is twice the radius.
![]() is a diameter. In this case, we would
have at least two of the three points on the same side of
is a diameter. In this case, we would
have at least two of the three points on the same side of ![]() on
on ![]() ; hence
we can suppose that
; hence
we can suppose that ![]() and
and ![]() both lie on the same side of
both lie on the same side of ![]() . However,
by the ruler axiom (Axiom 6), we must have
. However,
by the ruler axiom (Axiom 6), we must have
![]() since
since ![]() . This contradicts our assumption that
. This contradicts our assumption that ![]() and
and ![]() both lie
on
both lie
on ![]() .
.
![]() is not a diameter. We can assume that
is not a diameter. We can assume that ![]() lies between
lies between ![]() and
and ![]() on
on ![]() .
Draw the line segments,
.
Draw the line segments, ![]() ,
, ![]() ,
, ![]() . Then
. Then ![]() ,
, ![]() and
and ![]() are
triangles. In fact, since
are
triangles. In fact, since
![]() , they are isosceles
triangles. Let
, they are isosceles
triangles. Let ![]() be the measure of the base angles of triangle
be the measure of the base angles of triangle
![]() . Then it is also the measure of the base angle of
. Then it is also the measure of the base angle of
![]() , and
so it is also the measure of the base angle of
, and
so it is also the measure of the base angle of
![]() . Since the
two base angles at
. Since the
two base angles at ![]() add up to
add up to ![]() , we obtain that each of the three
triangles have two right angles, which is impossible.
, we obtain that each of the three
triangles have two right angles, which is impossible.
![]()
![]() is
is ![]() .
.
![]() and
and ![]() be two points on a circle of radius 1 and center
be two points on a circle of radius 1 and center ![]() .
The radii
.
The radii ![]() and
and ![]() make two angles
make two angles ![]() (the
``inner'' and the ``outer'' angles); call them
(the
``inner'' and the ``outer'' angles); call them ![]() and
and ![]() .
An angle such as
.
An angle such as ![]() whose vertex is at the center of the circle is
called a central angle. Notice that
whose vertex is at the center of the circle is
called a central angle. Notice that
![]() , no
matter where
, no
matter where ![]() and
and ![]() lie on
lie on ![]() .
If
.
If ![]() and
and ![]() are the endpoints of a diameter, they divide the circle into
two arcs, each of length
are the endpoints of a diameter, they divide the circle into
two arcs, each of length ![]() ; note also that the measure of the angles
; note also that the measure of the angles
![]() and
and ![]() are also
are also ![]() . In other cases, the length of the arc
subtended by the angle
. In other cases, the length of the arc
subtended by the angle ![]() will be whatever fraction of
will be whatever fraction of ![]() that
that
![]() is of the entire circle. For example, if
is of the entire circle. For example, if ![]() is a right
angle, it will take up
is a right
angle, it will take up ![]() of the circle, and the corresponding arc length
will be
of the circle, and the corresponding arc length
will be ![]() . We define the measure of the angle to be the corresponding
arc length when that angle is the central angle of a circle of radius 1.
. We define the measure of the angle to be the corresponding
arc length when that angle is the central angle of a circle of radius 1.
![]() and
and ![]() be the midpoints of sides
be the midpoints of sides ![]() and
and ![]() respectively. Draw
the perpendicular bisectors of
respectively. Draw
the perpendicular bisectors of ![]() and
and ![]() , and let
, and let ![]() be the point where
these two lines meet (note that
be the point where
these two lines meet (note that ![]() need not be inside the triangle). Draw
the lines
need not be inside the triangle). Draw
the lines ![]() ,
, ![]() and
and ![]() .
.
![]() , then we repeat the above argument to show that
, then we repeat the above argument to show that
![]() , from which, as above, it follows that
, from which, as above, it follows that
![]() . Again, this shows that there is a circumscribed circle.
. Again, this shows that there is a circumscribed circle.
![]()
![]()
![]() . Hence
. Hence
![]() .
.
![]()
![]() , then its center lies at the point of intersection of the three angle
bisectors, and its radius is the distance from this point to the three
sides. Hence we have proven the following.
, then its center lies at the point of intersection of the three angle
bisectors, and its radius is the distance from this point to the three
sides. Hence we have proven the following.
![]() . Similarly,
. Similarly,
![]() and
and
![]() .
.
![]() to the three sides all have
equal length; call this length
to the three sides all have
equal length; call this length ![]() . then the circle centered at
. then the circle centered at ![]() of
radius
of
radius ![]() is tangent to the three sides of
is tangent to the three sides of
![]() exactly at the
points
exactly at the
points ![]() ,
, ![]() and
and ![]() .
.
![]()