

Next: About this document ...
Up: MAT 200 Course Notes on
Previous: 5 Circles and lines
Subsections
Fill in the steps in the construction below, and observe the result.
- Start with arbitrary triangle
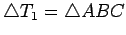 .
.
- Construct the lines
 ,
, 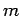 and
and 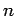 , parallel to
, parallel to  ,
,  and
and 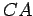 , respectively.
, respectively.
- These three lines form a new triangle,
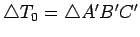 ; label these so that
; label these so that 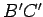 is parallel to
is parallel to  ,
, 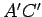 is parallel to
is parallel to 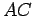 and
and 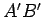 is parallel to
is parallel to  .
.
- Observe that the sides of
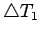 divide
divide
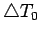 into four triangles.
into four triangles.
- Since the sides are parallel, these four triangles are all similar to the big triangle; in particular,
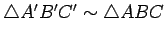 .
.
- Since they have some sides in common, the four smaller triangles are all congruent.
- It follows that
 is the midpoint of
is the midpoint of 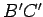 ;
;  is the midpoint of
is the midpoint of 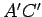 ; and
; and  is the midpoint of
is the midpoint of 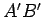 .
.
- Construct the perpendicular bisectors of
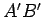 ,
, 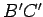 and
and 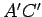 ; we know these all meet at a point ; call it
; we know these all meet at a point ; call it  . (
. ( is the center of the circumscribed circle for
is the center of the circumscribed circle for
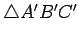 ; this center is called the orthocenter).
; this center is called the orthocenter).
- The lines
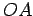 ,
, 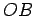 and
and 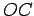 , when extended, are altitudes of
, when extended, are altitudes of
 .
.
- We have shown that the three altitudes of an arbitrary triangle meet at a point.
- Let
 be an arbitrary triangle.
be an arbitrary triangle.
- Let
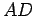 and
and 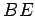 be medians. Let
be medians. Let 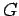 be the point of intersection of these two lines.
be the point of intersection of these two lines.
- Draw the line
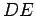 .
.
- Observe that
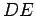 is parallel to
is parallel to  . (This was part of a homework assignment.)
. (This was part of a homework assignment.)
- Then
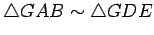 .
.
- We know that
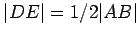 . Hence,
. Hence,
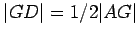 and
and
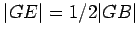 .
.
- Repeat the above argument, using the medians from
 and
and  .
.
- Conclude that the three medians of an arbitrary triangle meet at a point. (This point is called the centroid of the triangle; it is at the center of gravity.)
- We also have shown that the centroid divides each median into two segments; the segment between the centroid and the vertex is twice as long as the segment between the centroid and the opposite side.
Two circles  and
and  either are disjoint, or they meet at a point, in which case they are said to be tangent, or they meet at two points, in which case, they intersect.
either are disjoint, or they meet at a point, in which case they are said to be tangent, or they meet at two points, in which case, they intersect.
It is essentially immediate that two circles with the same center but different radii are disjoint.
Since a line is the shortest distance between two points, if we have two circles where the distance between the centers is greater than the sum of their radii, then the circles are necessarily disjoint.
If we have two circles with the property that the distance between their centers is exactly equal to the sum of their radii, then the line between their centers contains a point on both circles.
Proposition 6.1
If two circles have three points in common, then they are identical.
Proof.
Label the three points as

,

and

, and draw the lines

,

and
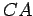
.
The three points cannot be collinear, for a line intersects a circle in at most two points. Since the three points are not collinear they form a triangle. Then both circles are circumscribed about
 . Since the circumscribed circle about a triangle is unique, the two circles are the same.
. Since the circumscribed circle about a triangle is unique, the two circles are the same.

Proposition 6.2
Suppose the circles  and
and  intersect at the points
intersect at the points  and
and  . Let
. Let  be the center of
be the center of  and let
and let 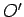 be the center of
be the center of  . Then the line
. Then the line 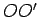 is the perpendicular bisector of the line segment
is the perpendicular bisector of the line segment  .
.
Proof.
Since

is a chord of

(

), the perpendicular bisector of the chord

passes through the center

(
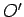
). Hence the perpendicular bisector of the line segment

is the line determined by

and
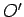
.

Proposition 6.3
Suppose the circles  and
and  are tangent at
are tangent at  . Then the line connecting the centers of these circles, passes through
. Then the line connecting the centers of these circles, passes through  .
.
Proof.
Let

be the center of

and let
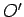
be the center of

. Suppose the line
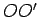
does not pass through

. Construct the perpendicular from

to the line
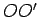
, and let

be the point where this perpendicular bisector meets
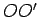
. Now construct the point

on the line

so that

lies between

and

and so that
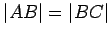
. Then, by
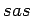
,
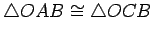
. Hence
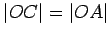
, from which it follows that

lies on

. Using the same argument,
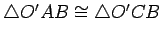
, from which it follows that

lies on

. We have constructed a second point of intersection of

and

; since we assumed these circles had only one point in common, we have reached a contradiction.

Corollary 6.4
If the circles  and
and  are tangent at
are tangent at  , and
, and  is the line tangent to
is the line tangent to  at
at  , then
, then  is tangent to
is tangent to  .
.
Proof.
Since

and

are tangent at

the line
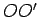
connecting their centers passes through

. Hence the radius of

at

lies on the line
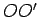
, and so
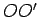
is orthogonal to

. The same argument shows that the radius of

lies on the line
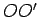
. Since the tangent to

at

is the line orthogonal to the radius at

, it is

.

We now return to the case of intersecting circles. Suppose the circles  and
and  intersect at the points
intersect at the points  and
and  . Then the line joining the centers
. Then the line joining the centers  and
and 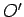 is the perpendicular bisector of the line segment
is the perpendicular bisector of the line segment  . We draw the radii,
. We draw the radii, 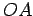 ,
, 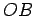 ,
, 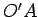 and
and 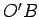 . We define the angle of intersection of these two circles at
. We define the angle of intersection of these two circles at  to be
to be
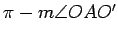 . Likewise, the angle of intersection at
. Likewise, the angle of intersection at  is
is
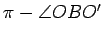 .
.
Remark: We could have chosen the angle between the circles to be
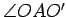 . The reason for our choice is that, if two circles are tangent, and each lies outside the other, then, by continuity, the angle between them is 0, while if one lies inside the other, then the angle between them is
. The reason for our choice is that, if two circles are tangent, and each lies outside the other, then, by continuity, the angle between them is 0, while if one lies inside the other, then the angle between them is 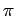 .
.
Proposition 6.5
If the circles  and
and  intersect at
intersect at  and
and  , then the angle of intersection at
, then the angle of intersection at  has the same measure as the angle of intersection at
has the same measure as the angle of intersection at  .
.
Since the angle of intersection at  and the angle of intersection at
and the angle of intersection at  have the same measure, we can simply call it the angle of intersection of the two circles.
have the same measure, we can simply call it the angle of intersection of the two circles.
We remark that, since the tangent to  at
at  is orthogonal to
is orthogonal to 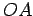 , and the tangent to
, and the tangent to  at
at  is orthogonal to
is orthogonal to 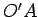 , then the angle between the lines
, then the angle between the lines 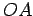 and
and 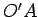 has the same measure as one of the angles between these tangents.
has the same measure as one of the angles between these tangents.
Proposition 6.6
Suppose we are given three positive real number, 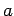 ,
, 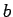 and
and 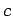 , where
, where 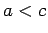 ,
, 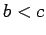 and
and 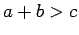 . Then there is a triangle with sides
. Then there is a triangle with sides 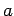 ,
, 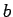 and
and 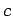 .
.
Two circles are orthogonal if the angle between them is 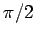 .
.
Proposition 6.7
Let  be a circle with center
be a circle with center  and radius
and radius 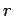 . Let
. Let  be some point on
be some point on  , and let
, and let 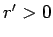 be any real number. Then there is a unique circle
be any real number. Then there is a unique circle  of radius
of radius 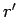 , orthogonal to
, orthogonal to  , where the center
, where the center 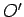 of
of  lies on the line
lies on the line 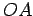 , and
, and 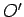 lies on the same side of
lies on the same side of  as does
as does  .
.
Proof.
We first prove uniqueness. Suppose we have such a circle

. Let

be one of the two points of intersection of

and

. Then the triangle
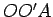
is a right triangle with right angle at

. Hence, by the Pythagorean theorem,
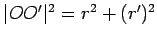
. This shows that the distance from

to
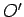
is determined; hence the circle

is determined.
To prove existence, find the point 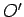 on
on 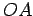 , on the same side of
, on the same side of  as
as  , and at distance
, and at distance
from

. Then construct the circle

of radius
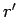
at that point.
To show that  and
and  intersect, it suffices to show that there is a point
intersect, it suffices to show that there is a point  on both
on both  and
and  , or equivalently, that there is a triangle with side lengths,
, or equivalently, that there is a triangle with side lengths, 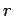 ,
, 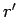 and
and 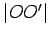 . This follows from the above proposition, once we observe that
. This follows from the above proposition, once we observe that
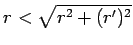 ,
,
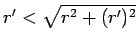 , and
, and
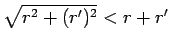 .
.

We remark without proof that, given two orthogonal circles  and
and  , there is a 1-parameter family of circles orthogonal to both
, there is a 1-parameter family of circles orthogonal to both  and
and  . However, given three mutually orthogonal circles, there is no fourth circle orthogonal to all three.
. However, given three mutually orthogonal circles, there is no fourth circle orthogonal to all three.
Proposition 6.8
Let  be a given circle of radius
be a given circle of radius 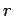 and center
and center  . Let
. Let  be any point, where
be any point, where 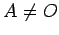 and
and  does not lie on
does not lie on  . Then there is a circle
. Then there is a circle  , centered at
, centered at  , where
, where  and
and  are tangent.
are tangent.
Proof.
Draw the line
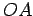
. This line intersects

in two points; let

be one of them. Draw the circle

of radius
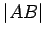
about

. This circle certainly meets

at

. Since

lies on the line connecting the centers of the circles, the circles are tangent at

.

We remark that we have in fact shown that there are exactly two circles centered at  that are tangent to
that are tangent to  .
.
There are three possible orientations for the two tangent circle. We can have that  lies outside
lies outside  and
and  lies outside
lies outside  , or we can have that
, or we can have that  lies inside
lies inside  , or we can have that
, or we can have that  lies inside
lies inside  .
.
Exercise: Suppose  ,
,  and
and  are three given points on a line. How many distinct triples of mutually tangent circles are there, where one of the circles is centered at
are three given points on a line. How many distinct triples of mutually tangent circles are there, where one of the circles is centered at  , one is centered at
, one is centered at  , and the third is centered at
, and the third is centered at  .
.
Proposition 6.9
Let
 be given. Then there are three mutually tangent circles,
be given. Then there are three mutually tangent circles, 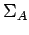 centered at
centered at  ,
, 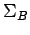 centered at
centered at  , and
, and 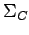 centered at
centered at  . If we require that each of the three circles lies outside the others, then the radii of these circles are determined by the lengths of the sides of the triangle.
. If we require that each of the three circles lies outside the others, then the radii of these circles are determined by the lengths of the sides of the triangle.
Proof.
We need to find the radii; call these
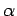
,
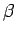
and
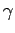
, where
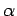
is the radius of
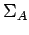
,
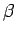
is the radius of
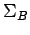
and
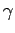
is the radius of
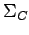
. Then we must solve the equations:
It is an exercise in linear algebra to show that these equations have a unique solution.

We close with the remark that, given three mutually tangent circles, there exist exactly two disjoint circles that are tangent to all three. If one has four mutually tangent circles, then there can be no fifth.


Next: About this document ...
Up: MAT 200 Course Notes on
Previous: 5 Circles and lines
Scott Sutherland
2002-12-18
![]() . Since the circumscribed circle about a triangle is unique, the two circles are the same.
. Since the circumscribed circle about a triangle is unique, the two circles are the same.
![]()
![]() . The reason for our choice is that, if two circles are tangent, and each lies outside the other, then, by continuity, the angle between them is 0, while if one lies inside the other, then the angle between them is
. The reason for our choice is that, if two circles are tangent, and each lies outside the other, then, by continuity, the angle between them is 0, while if one lies inside the other, then the angle between them is ![]() .
.
![]() ,
,
![]() and
and
![]() . It follows that
. It follows that
![]() and that
and that
![]() . Hence
. Hence
![]() .
.
![]()
![]() and the angle of intersection at
and the angle of intersection at ![]() have the same measure, we can simply call it the angle of intersection of the two circles.
have the same measure, we can simply call it the angle of intersection of the two circles.
![]() at
at ![]() is orthogonal to
is orthogonal to ![]() , and the tangent to
, and the tangent to ![]() at
at ![]() is orthogonal to
is orthogonal to ![]() , then the angle between the lines
, then the angle between the lines ![]() and
and ![]() has the same measure as one of the angles between these tangents.
has the same measure as one of the angles between these tangents.
![]() , the point
, the point ![]() lies outside the circle centered at
lies outside the circle centered at ![]() , and since
, and since ![]() , the point
, the point ![]() lies outside the circle centered at
lies outside the circle centered at ![]() . Hence neither circle lies inside the other, and so the circles intersect. Let
. Hence neither circle lies inside the other, and so the circles intersect. Let ![]() be one of the points of intersection, and observe that
be one of the points of intersection, and observe that ![]() and
and ![]() .
.
![]()
![]() on
on ![]() , on the same side of
, on the same side of ![]() as
as ![]() , and at distance
, and at distance
![]() and
and ![]() intersect, it suffices to show that there is a point
intersect, it suffices to show that there is a point ![]() on both
on both ![]() and
and ![]() , or equivalently, that there is a triangle with side lengths,
, or equivalently, that there is a triangle with side lengths, ![]() ,
, ![]() and
and ![]() . This follows from the above proposition, once we observe that
. This follows from the above proposition, once we observe that
![]() ,
,
![]() , and
, and
![]() .
.
![]()
![]() and
and ![]() , there is a 1-parameter family of circles orthogonal to both
, there is a 1-parameter family of circles orthogonal to both ![]() and
and ![]() . However, given three mutually orthogonal circles, there is no fourth circle orthogonal to all three.
. However, given three mutually orthogonal circles, there is no fourth circle orthogonal to all three.
![]() lies outside
lies outside ![]() and
and ![]() lies outside
lies outside ![]() , or we can have that
, or we can have that ![]() lies inside
lies inside ![]() , or we can have that
, or we can have that ![]() lies inside
lies inside ![]() .
.
![]() ,
, ![]() and
and ![]() are three given points on a line. How many distinct triples of mutually tangent circles are there, where one of the circles is centered at
are three given points on a line. How many distinct triples of mutually tangent circles are there, where one of the circles is centered at ![]() , one is centered at
, one is centered at ![]() , and the third is centered at
, and the third is centered at ![]() .
.
![]()