

Next: 3 The parallel axiom
Up: MAT 200 Course Notes on
Previous: 1 Introduction
Subsections
Three distinct lines, 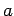 ,
, 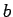 and
and
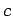 , no two of which are parallel, form a triangle. That is,
they divide the plane into some number of regions; exactly one of
them, the triangle, is bounded, and has segments of all three lines on
its boundary.
, no two of which are parallel, form a triangle. That is,
they divide the plane into some number of regions; exactly one of
them, the triangle, is bounded, and has segments of all three lines on
its boundary.
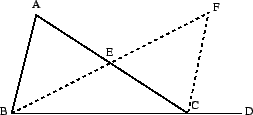
The triangle with vertices 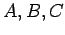 is denoted by
is denoted by
 , where
, where  is the point of intersection of the lines
is the point of intersection of the lines 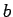 and
and 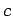 ;
;
 is the point of intersection of the lines
is the point of intersection of the lines 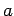 and
and 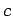 ; and
; and  is
the point of intersection of the lines
is
the point of intersection of the lines 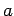 and
and 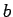 . These points of
intersection divide each of the lines into two unbounded half-lines
and one bounded line segment, called a side of the triangle.
. These points of
intersection divide each of the lines into two unbounded half-lines
and one bounded line segment, called a side of the triangle.
The triangle,
 , defines
, defines 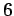 numbers, the angle measures
(also called the angles) at the vertices
numbers, the angle measures
(also called the angles) at the vertices  ,
,  and
and  , and the
lengths of the sides, which are the line segments
, and the
lengths of the sides, which are the line segments  ,
, 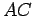 and
and  .
.
The angle measure at for example the vertex  is denoted by
is denoted by
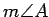 , or
, or
 .
.
The use of the phrase ``measure of an angle''
is relatively modern. Up to about 50 years ago, the measure of the angle at
 was simply denoted by
was simply denoted by  or
or 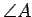 , and it was left to the reader
to distinguish between the angle and its measure. When convenient, we will
follow this convention, and use the same notation for an angle and its
measure.
, and it was left to the reader
to distinguish between the angle and its measure. When convenient, we will
follow this convention, and use the same notation for an angle and its
measure.
We will always give angle measures
in radians, so, if 
 and
and  all lie on a line, with
all lie on a line, with  between
between
 and
and  , then
, then
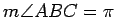 .
.
We denote the length of the side  , for example, by
, for example, by 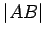 . Until
modern times, the side and its length were denoted by the same symbol,
and the reader had to figure out which is which from the context. As
with angles, when convenient, we will also use the same notation for a
line segment and its length.
. Until
modern times, the side and its length were denoted by the same symbol,
and the reader had to figure out which is which from the context. As
with angles, when convenient, we will also use the same notation for a
line segment and its length.
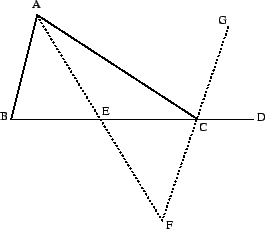
The pair of lines, 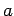 and
and 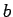 , for example, determines two angles;
the question of which of these angles is determined by the triangle
can be stated in words with difficulty; we will leave this as visually
obvious.
, for example, determines two angles;
the question of which of these angles is determined by the triangle
can be stated in words with difficulty; we will leave this as visually
obvious.
Two triangles,
 and
and
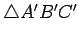 , are congruent if the corresponding angles have equal
measures, and the corresponding sides have equal lengths. That is, the
triangles,
, are congruent if the corresponding angles have equal
measures, and the corresponding sides have equal lengths. That is, the
triangles,
 and
and
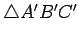 are congruent if
are congruent if
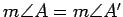 ;
;
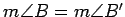 ;
;
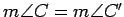 ;
;
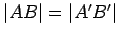 ;
;
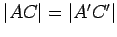 ; and
; and
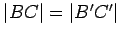 . In this case,
we write
. In this case,
we write
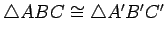 .
.
For physical triangles, two triangles are congruent if they exactly
match if you put one on top of the other. Another way of saying this,
for ideal triangles, is that there is an isometry of the plane (a
composition of rotation, translation and reflection) that maps one
exactly onto the other.
Exercise 2.1
Show that congruence of triangles is an equivalence
relation.
It is essentially obvious
that congruence of triangles is an equivalence relation. However, the
statement that
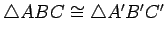 says nothing about
whether
says nothing about
whether
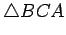 is or is not congruent to
is or is not congruent to
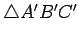 . More precisely, the statement
. More precisely, the statement
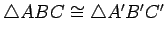 not only tells you that these two triangles are congruent, but
also tells you that
not only tells you that these two triangles are congruent, but
also tells you that
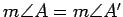 ,
,
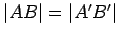 , etc.
, etc.
It is common to refer to the above angle as ``Angle-Side-Angle'' or ASA.
For physical triangles this is essentially obvious. If you know the
length of a side, and you know the two angles, then the lines on which
the other sides lie are determined, so the third vertex is also
determined.
A physical triangle is determined by 6 pieces of information, the 3 lengths
and the 3 angles.
There are 6 possible statements concerning 3 pieces of information. Convince
yourself that AAA and SSA are false, while AAS, ASA, SAS and SSS are true. (There is nothing here for you to hand in, but you need this
information for the next two questions.)
Remark: One of these, AAS, is not obvious; in fact it is false
in spherical geometry.
In the following few exercises, when you are asked to prove something you
may assume that AAS, ASA, SAS and SSS are true. One other fact that
you may use is Thm. 3.4: the sum of the angles of a
triangle is 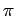 . Note that this is only for these exercises; in
general we cannot assume things we have not proven or taken as an axiom,
because we may wind up applying circular reasoning (that is, giving a proof
that something is true which implicitly assumes it was true to begin with.)
But the main point of this exercise is to get you thinking about how
geometry works, so we can relax our restrictions a little.
. Note that this is only for these exercises; in
general we cannot assume things we have not proven or taken as an axiom,
because we may wind up applying circular reasoning (that is, giving a proof
that something is true which implicitly assumes it was true to begin with.)
But the main point of this exercise is to get you thinking about how
geometry works, so we can relax our restrictions a little.
Exercise 2.2
Is it true that no 2 pieces of information suffice to
determine a triangle? That is, can you find two pieces of information
so that if you have any two triangles for which these two measurements
are the same, the triangles must necessarily be congruent.
Prove your answer.
Exercise 2.3
What about 4 pieces of information; i.e., do any four pieces of information
suffice for congruence of triangles? Prove your answer.
A quadrilateral is a region bounded by four line segments;
that is, it is a four-sided figure. The quadrilateral with vertices,
 ,
,  ,
,  and
and  , in this order, is determined by the four line
segments connecting
, in this order, is determined by the four line
segments connecting  and
and  ,
,  and
and  ,
,  and
and  , and connecting
, and connecting
 and
and  . For
. For 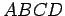 to form a quadrilateral, these segments must not
intersect except at the verticies.
to form a quadrilateral, these segments must not
intersect except at the verticies.
A quadrilateral defines 8 pieces of information: the lengths of the four
sides, and the measures of the four angles. Two quadrilaterals are
congruent if these 8 pieces of information agree.
What is the minimal number of pieces of information one needs about two
quadrilaterals to prove that they are congruent? (No response needed here,
but you need the answer for the next question.)
Exercise 2.4
State and prove one congruence theorem for quadrilaterals, where the
hypothesis consists of the minimal number of pieces of information.
Here are two more
axioms we shall need. Essentially, they say that for every real
number, a segment can be scaled to that length, and that angles can be
subdivided into angles of any measurement between 0 and 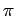 .
.
A triangle is isosceles if two of its sides have equal
length. The two sides of equal length are called legs; the point
where the two legs meet is called the apex of the triangle; the
other two angles are called the base angles of the triangle; and
the third side is called the base.
While an isosceles triangle is defined to be one with two sides of equal
length, the next theorem tells us that is equivalent to having two angles of
equal measure.
Exercise 2.5
Prove Theorem 2.2 by showing that
 is congruent
to its reflection
is congruent
to its reflection
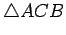 . Note that there are two parts to the
theorem, and so you need to give essentially two separate arguments.
. Note that there are two parts to the
theorem, and so you need to give essentially two separate arguments.
Proof.
If the two triangles were not congruent, then one of the angles of

would have measure different from the measure of the
corresponding angle of
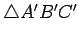
. If necessary, relabel the
triangles so that
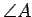
and
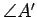
are two corresponding
angles which differ, with
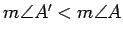
.
We find a point  and construct the line
and construct the line 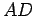 so that
so that
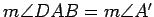 , and
, and
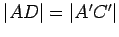 . (That this can be done follows
from Axioms 6 and 7.)
It is unclear where the point
. (That this can be done follows
from Axioms 6 and 7.)
It is unclear where the point  lies:
it could lie inside triangle
lies:
it could lie inside triangle 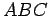 ;
it could lie on the line
;
it could lie on the line  between
between  and
and  ;
or it could lie on the other side of the line
;
or it could lie on the other side of the line  .
We need to take up these three cases separately.
.
We need to take up these three cases separately.
Exercise 2.6
Suppose the point  lies on the line
lies on the line  . Explain why this yields an
immediate contradiction.
. Explain why this yields an
immediate contradiction.
For both of the remaining cases, we draw the lines 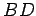 and
and 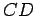 . We
observe that, by SAS,
. We
observe that, by SAS,
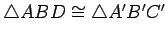 . It
follows that
. It
follows that
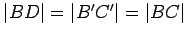 and that
and that
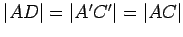 . Hence
. Hence
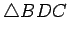 is isosceles, with base
is isosceles, with base 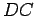 , and
, and
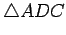 is
isosceles with base
is
isosceles with base 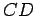 . Since the base angles of an isosceles
triangle have equal measure,
. Since the base angles of an isosceles
triangle have equal measure,
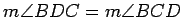 and
and
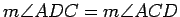 .
.
First, we take up the case that

lies outside

;
that is,

lies on the other side of the line

from

.
Exercise 2.7
Finish this case of the proof, first by showing that
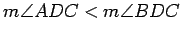 and
and
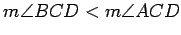 .
Then use the isosceles triangles to arrive at the contradiction
that
.
Then use the isosceles triangles to arrive at the contradiction
that
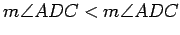 .
.
We now consider the case where

lies inside

. Extend the line

to some point
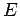
. Observe that
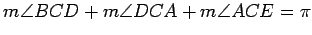
, from which it follows that
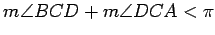
. Next, extend the line
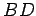
past

to some
point
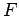
. Also extend the line
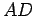
past the point

to some point
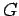
, and extend the line
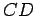
past the point

to some point
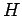
.
Exercise 2.8
Finish this case of the proof by explaining why
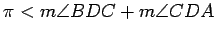 and
and
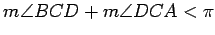 , and
then show that this leads to the contradiction
, and
then show that this leads to the contradiction 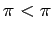 .
.

Proof.
We first prove part (i). Let
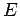
be the midpoint of the line segment
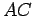
; that is,
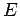
lies on the line
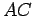
, between

and

, and
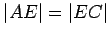
. Draw the line
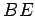
and extend it past
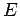
to the point
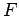
, so that
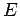
is the midpoint of
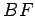
. Also draw the line
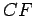
.
Exercise 2.9
Finish the proof of part (i). Hint: First show that
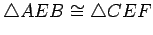 (Thm. 1.1 may be useful.)
Use that to compare
(Thm. 1.1 may be useful.)
Use that to compare 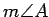 and
and
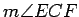 , and conclude that
, and conclude that
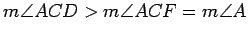 .
.
For part (ii), we choose
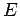
to be the midpoint of the line

, and
extend
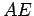
beyond
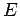
to
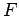
, so that
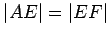
.
Also, extend the line Now extend the line
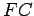
beyond

to some point
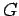
.
Exercise 2.10
Finish the proof of part (ii).
First show that
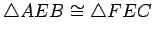 , and then
compare
, and then
compare
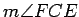 ,
,
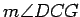 ,
,
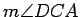 , and
, and 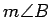 .
.

The next theorem says that in a triangle, if one angle is bigger than
another, the side opposite the bigger angle must be longer than the one
opposite the smaller angle. This is generalizes the fact that the base
angles of isosceles triangles are equal (Thm. 2.2).
Proof.
Assume not. Then either
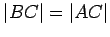
or
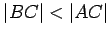
.
Exercise 2.11
Show that if 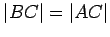 , the assumption
, the assumption
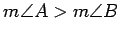 is
contradicted.
is
contradicted.
Exercise 2.12
Now assume 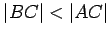 , find the point
, find the point  on
on 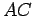 so that
so that
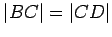 , and draw the line
, and draw the line 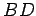 . Finish the proof in this case.
Hint:
Use Thm. 2.4 and the fact that
. Finish the proof in this case.
Hint:
Use Thm. 2.4 and the fact that 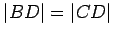 to
conclude that
to
conclude that
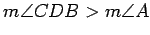 . Now observe that
. Now observe that
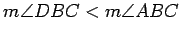 . Explain why this gives the contradiction
. Explain why this gives the contradiction
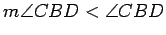 .
.

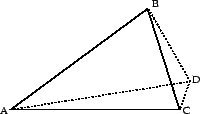
The converse of the previous theorem is also true: opposite a long side,
there must be a big angle.
Proof.
Assume not. If
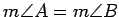
, then

is isosceles,
with apex at

, so
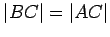
, which contradicts our assumption.
If
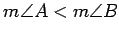 , then, by the previous theorem,
, then, by the previous theorem, 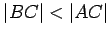 , which
again contradicts our assumption.
, which
again contradicts our assumption.

The following theorem doesn't quite say that a straight line is the shortest
distance between two points, but it says something along these lines. This
result is used throughout much of mathematics, and is referred to as ``the
triangle inequality''.
Exercise 2.13
Prove the triangle inequality: First extend  to a point
to a point  so
that
so
that 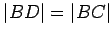 , then form the isosceles triangle
, then form the isosceles triangle
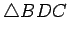 .
Use this triangle and Thm 2.2 to show that
.
Use this triangle and Thm 2.2 to show that
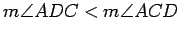 . Conclude that
. Conclude that
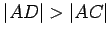 by using
another theorem from this section. Then show that
by using
another theorem from this section. Then show that
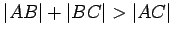 .
.
Proof.
We first observe that, by either
SAS or
ASA, if
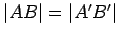
, then
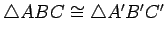
. Hence we
can assume that
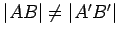
, from which it follows that either
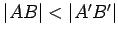
or
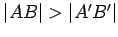
. We can assume without loss of
generality that
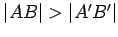
(that is, if we had that
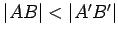
, then we would interchange the labelling of the two
triangles).
Now find the point

between

and

, so that
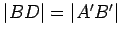
. Observe that, by
SAS,
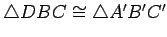
. Hence
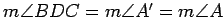
. This contradicts
that fact that, since
is an exterior angle for
, we must have that
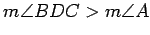
.

This concludes the generalities concerning congruence of triangles. We
now know the four congruence theorems, ASA, SAS, SSS and AAS. We
also know that the other two possibilities, SSA and AAA, are not
valid. It follows that, for example, if we are given the lengths of
all three sides of a triangle, then the measures of all three angles
are determined. However, we do not as yet have any means of computing
the measures of these angles in terms of the lengths of the sides.
Two lines intersecting at a point  are perpendicular or
orthogonal if all four angles at
are perpendicular or
orthogonal if all four angles at  are equal. In this case,
each of the angles has measure
are equal. In this case,
each of the angles has measure 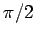 . These angles are called
right angles. It is standard in mathematics to use the words
perpendicular and orthogonal interchangeably.
. These angles are called
right angles. It is standard in mathematics to use the words
perpendicular and orthogonal interchangeably.
BASIC CONSTRUCTION.
Given a line  , and any point
, and any point  , there is a line through
, there is a line through  perpendicular to
perpendicular to  .
.
Exercise 2.14
Prove that the line through  perpendicular to
perpendicular to  is unique. (Note that
is unique. (Note that  may or may not lie on
may or may not lie on  .)
.)
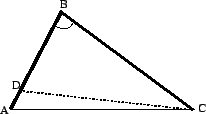
In any triangle, there are three special lines from each vertex. In
 , the altitude from
, the altitude from  is perpendicular to
is perpendicular to
 ; the median from
; the median from  bisects
bisects  (that is, it crosses
(that is, it crosses
 at a point
at a point  so that
so that 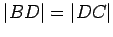 ); and the angle
bisector bisects
); and the angle
bisector bisects 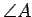 (that is, if
(that is, if 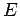 is the point where the
angle bisector meets
is the point where the
angle bisector meets  , then
, then
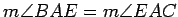 ).
).
Theorem 2.9
If  is the apex of the isosceles triangle
is the apex of the isosceles triangle 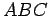 , and
, and
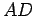 is the altitude, then
is the altitude, then 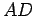 is also the median, and is also the
angle bisector, from
is also the median, and is also the
angle bisector, from  .
.
Exercise 2.15
Prove this theorem. (Hint: Construct the altitude and apply AAS to the
pair of resulting triangles.)
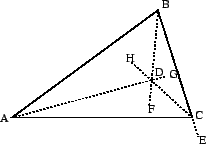
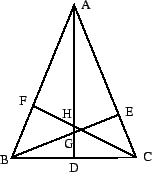
Theorem 2.10
In an isosceles triangle, the three altitudes meet at a point.
Proof.
Let

be the apex of the isosceles

, and let
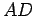
be
the altitude, which is also the median and the angle
bisector. Similarly, let
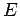
be the endpoint on
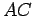
of the altitude
from

, and let
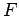
be the endpoint on

of the altitude from

.
Let
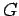
be the point of intersection of
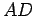
with
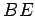
, and let
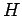
be
the point of intersection of
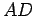
with
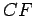
. We need to prove that
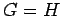
.
By AAS,
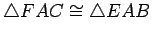 . Hence
. Hence 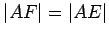 . Since
. Since
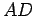 is also the angle bisector, by ASA,
is also the angle bisector, by ASA,
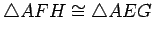 . Hence
. Hence 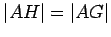 , from which it follows that
, from which it follows that 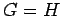 .
.

Exercise 2.16
Prove that the three angle bisectors in an isosceles triangle meet at a point.
Exercise 2.17
Prove that the three medians in an isosceles triangle meet at a point.


Next: 3 The parallel axiom
Up: MAT 200 Course Notes on
Previous: 1 Introduction
Scott Sutherland
2002-12-18
![]() is denoted by
is denoted by
![]() , where
, where ![]() is the point of intersection of the lines
is the point of intersection of the lines ![]() and
and ![]() ;
;
![]() is the point of intersection of the lines
is the point of intersection of the lines ![]() and
and ![]() ; and
; and ![]() is
the point of intersection of the lines
is
the point of intersection of the lines ![]() and
and ![]() . These points of
intersection divide each of the lines into two unbounded half-lines
and one bounded line segment, called a side of the triangle.
. These points of
intersection divide each of the lines into two unbounded half-lines
and one bounded line segment, called a side of the triangle.
![]() , defines
, defines ![]() numbers, the angle measures
(also called the angles) at the vertices
numbers, the angle measures
(also called the angles) at the vertices ![]() ,
, ![]() and
and ![]() , and the
lengths of the sides, which are the line segments
, and the
lengths of the sides, which are the line segments ![]() ,
, ![]() and
and ![]() .
.
![]() is denoted by
is denoted by
![]() , or
, or
![]() .
.
![]() , for example, by
, for example, by ![]() . Until
modern times, the side and its length were denoted by the same symbol,
and the reader had to figure out which is which from the context. As
with angles, when convenient, we will also use the same notation for a
line segment and its length.
. Until
modern times, the side and its length were denoted by the same symbol,
and the reader had to figure out which is which from the context. As
with angles, when convenient, we will also use the same notation for a
line segment and its length.
![]() and
and ![]() , for example, determines two angles;
the question of which of these angles is determined by the triangle
can be stated in words with difficulty; we will leave this as visually
obvious.
, for example, determines two angles;
the question of which of these angles is determined by the triangle
can be stated in words with difficulty; we will leave this as visually
obvious.
![]() . Note that this is only for these exercises; in
general we cannot assume things we have not proven or taken as an axiom,
because we may wind up applying circular reasoning (that is, giving a proof
that something is true which implicitly assumes it was true to begin with.)
But the main point of this exercise is to get you thinking about how
geometry works, so we can relax our restrictions a little.
. Note that this is only for these exercises; in
general we cannot assume things we have not proven or taken as an axiom,
because we may wind up applying circular reasoning (that is, giving a proof
that something is true which implicitly assumes it was true to begin with.)
But the main point of this exercise is to get you thinking about how
geometry works, so we can relax our restrictions a little.
![]() ,
, ![]() ,
, ![]() and
and ![]() , in this order, is determined by the four line
segments connecting
, in this order, is determined by the four line
segments connecting ![]() and
and ![]() ,
, ![]() and
and ![]() ,
, ![]() and
and ![]() , and connecting
, and connecting
![]() and
and ![]() . For
. For ![]() to form a quadrilateral, these segments must not
intersect except at the verticies.
to form a quadrilateral, these segments must not
intersect except at the verticies.
![]() (if
not, just exchange the names on the triangles).
(if
not, just exchange the names on the triangles).
![]() and some point
and some point ![]() lying between
lying between
![]() and
and ![]() , so that
, so that
![]() .
.
![]() . Therefore
. Therefore
![]() . But we are given that
. But we are given that
![]() . Therefore,
. Therefore,
![]() . Since
. Since ![]() lies on the line determined by
lies on the line determined by ![]() and
and ![]() , and lies
between them, this contradicts Axiom 6.
, and lies
between them, this contradicts Axiom 6.
![]()
![]() has
has
![]() , then it is
isosceles, with base
, then it is
isosceles, with base ![]() .
.![]() and construct the line
and construct the line ![]() so that
so that
![]() , and
, and
![]() . (That this can be done follows
from Axioms 6 and 7.)
It is unclear where the point
. (That this can be done follows
from Axioms 6 and 7.)
It is unclear where the point ![]() lies:
it could lie inside triangle
lies:
it could lie inside triangle ![]() ;
it could lie on the line
;
it could lie on the line ![]() between
between ![]() and
and ![]() ;
or it could lie on the other side of the line
;
or it could lie on the other side of the line ![]() .
We need to take up these three cases separately.
.
We need to take up these three cases separately.
![]() and
and ![]() . We
observe that, by SAS,
. We
observe that, by SAS,
![]() . It
follows that
. It
follows that
![]() and that
and that
![]() . Hence
. Hence
![]() is isosceles, with base
is isosceles, with base ![]() , and
, and
![]() is
isosceles with base
is
isosceles with base ![]() . Since the base angles of an isosceles
triangle have equal measure,
. Since the base angles of an isosceles
triangle have equal measure,
![]() and
and
![]() .
.
![]()
![]()
![]() , then, by the previous theorem,
, then, by the previous theorem, ![]() , which
again contradicts our assumption.
, which
again contradicts our assumption.
![]()
![]()
![]() , and any point
, and any point ![]() , there is a line through
, there is a line through ![]() perpendicular to
perpendicular to ![]() .
.
![]() , the altitude from
, the altitude from ![]() is perpendicular to
is perpendicular to
![]() ; the median from
; the median from ![]() bisects
bisects ![]() (that is, it crosses
(that is, it crosses
![]() at a point
at a point ![]() so that
so that ![]() ); and the angle
bisector bisects
); and the angle
bisector bisects ![]() (that is, if
(that is, if ![]() is the point where the
angle bisector meets
is the point where the
angle bisector meets ![]() , then
, then
![]() ).
).
![]() . Hence
. Hence ![]() . Since
. Since
![]() is also the angle bisector, by ASA,
is also the angle bisector, by ASA,
![]() . Hence
. Hence ![]() , from which it follows that
, from which it follows that ![]() .
.
![]()