
Next: 4 Lengths, areas and
Up: MAT 200 Course Notes on
Previous: 2 Triangles and congruence
Subsections
We remark that the point of the axiom is not the existence of the
parallel, but the uniqueness. We will see below that existence
actually follows from what we already know.
It is sometimes convenient to think of a line as being parallel to itself,
so we make the following formal definition. Two lines are not parallel if
they have exactly one point in common; otherwise they are parallel.
Theorem 3.1
In the set of all lines in the plane, the relation of being parallel is an
equivalence relation.
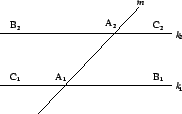
We will meet the following situation
some number of times. We are given two lines 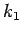 and
and 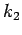 , and a third
line
, and a third
line 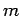 , where
, where 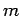 crosses
crosses 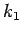 at
at 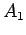 and
and 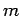 crosses
crosses 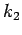 at
at
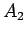 . Choose a point
. Choose a point
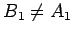 on
on 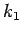 , and choose a point
, and choose a point
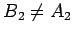 on
on 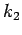 , where
, where 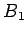 and
and 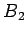 lie on opposite sides of the line
lie on opposite sides of the line
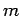 . Then
. Then
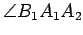 and
and
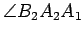 are referred to as
alternate interior angles.
are referred to as
alternate interior angles.
In any given situation, there are two distinct pairs of alternate interior
angles. That is, let 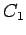 be some point on
be some point on 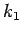 , where
, where 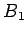 and
and 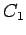 lie
on opposite sides of
lie
on opposite sides of 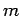 , and let
, and let 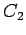 be some point on
be some point on 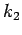 , where
, where 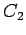 and
and 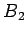 lie on opposite sides of
lie on opposite sides of 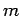 . Then one could also regard
. Then one could also regard
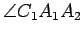 and
and
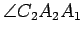 as being alternate interior
angles. However, observe that
as being alternate interior
angles. However, observe that
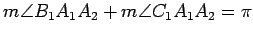 and
and
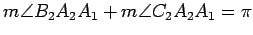 . It follows that one pair of
alternate interior angles are equal if and only if the other pair of
alternate interior angles are equal.
. It follows that one pair of
alternate interior angles are equal if and only if the other pair of
alternate interior angles are equal.
Proposition 3.2
If the alternate interior angles are equal, then the lines
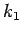 and
and 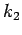 are parallel.
are parallel.
Proof.
Suppose not. Then the lines
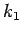
and
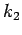
meet at some point

. If
necessary, we interchange the roles of the
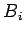
and the
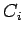
so that
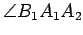
is an exterior angle of
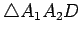
. Then

and
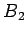
lie on the same side of
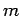
, so
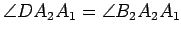
. By
the exterior angle inequality,
so we have reached a contradiction.

Let 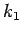 be a line, and let
be a line, and let 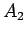 be a point not on
be a point not on 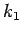 . Pick some point
. Pick some point 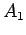 on
on 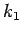 and draw the line
and draw the line
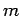 through
through 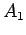 and
and 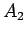 . By Axiom 7, we can find a line
. By Axiom 7, we can find a line 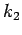 through
through
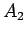 so that the alternate interior angles are equal. Hence we can find a
line through
so that the alternate interior angles are equal. Hence we can find a
line through 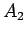 parallel to
parallel to 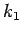 .
.
Theorem 3.3 (alternate interior angles equal)
Two lines 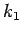 and
and 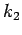 are parallel if and only if the alternate
interior angles are equal.
are parallel if and only if the alternate
interior angles are equal.
Proof.
To prove the forward direction, construct the line
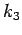
through
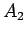
,
where there is a point
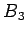
on
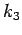
, with
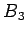
and
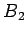
on the same
side of
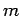
, so that
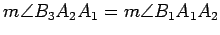
. Then, by
Prop.
3.2,
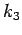
is a line through
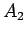
parallel to
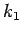
. Axiom
8 implies
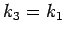
. Hence
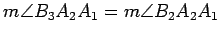
, and the desired conclusion follows.
The other direction is just Prop. 3.2,
restated as part of this theorem for convenience.

Theorem 3.4
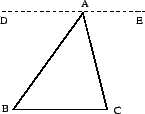
The sum of the measures of the angles of a triangle is equal to 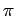 .
.
Proof.
Consider

, and let
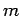
be the line passing through

and
parallel to

. Let

and
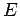
be two points on
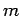
, on opposite sides of

, where

and

lie on opposite sides of the line

. Then

and
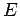
lie on opposite sides of
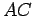
.
Exercise 3.1
Use alternate interior angles to complete the proof of this theorem.

A quadrilateral is a region bounded by four line segments, so it
has four verticies on its boundary.
Corollary 3.5
The sum of the measures of the angles of a quadrilateral is 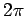 .
.
Proof.
Cut the triangle into two triangles, and do the obvious computation.

A rectangle is a quadrilateral in which all four angles are right
angles.
Theorem 3.6
If 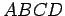 is a rectangle, then
is a rectangle, then  is parallel to
is parallel to 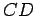 , and
, and
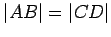 . Similarly,
. Similarly,  is parallel to
is parallel to 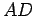 and
and 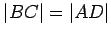 .
.
Exercise 3.2
Prove this theorem.
- i.
- Prove that opposite pairs of sides are parallel.
- ii.
- Now cut the rectangle into two triangles; prove that these two
triangles are congruent. Conclude that opposite sides of the rectangle have
equal length.
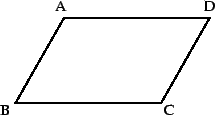
Somewhat more generally, a parallelogram is a quadrilateral 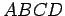 in which opposite sides are parallel; that is,
in which opposite sides are parallel; that is,  is parallel to
is parallel to 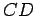 , and
, and
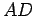 is parallel to
is parallel to  .
.
A rectangle with all four sides of equal length is a square; a
parallelogram with all four sides of equal length is a rhombus.
Exercise 3.3
Prove this theorem. (Hint: Draw a diagonal.)
Theorem 3.8
If 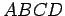 is a quadrilateral in which
is a quadrilateral in which 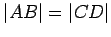 and
and 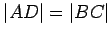 , then
, then
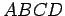 is a parallelogram.
is a parallelogram.
Exercise 3.4
Prove this theorem.
Theorem 3.9
Let 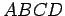 be a parallelogram with diagonals of equal length (that is,
be a parallelogram with diagonals of equal length (that is,
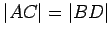 ). Then
). Then 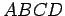 is a rectangle.
is a rectangle.
Exercise 3.5
Prove this theorem.


Next: 4 Lengths, areas and
Up: MAT 200 Course Notes on
Previous: 2 Triangles and congruence
Scott Sutherland
2002-12-18
![]() is parallel to
is parallel to ![]() , and
, and ![]() is parallel to
is parallel to ![]() . There is
obviously nothing further to prove unless the three lines are
distinct. Assume that
. There is
obviously nothing further to prove unless the three lines are
distinct. Assume that ![]() and
and ![]() are not parallel. Since two lines are
either equal, parallel, or have exactly one point in common, we must have
that
are not parallel. Since two lines are
either equal, parallel, or have exactly one point in common, we must have
that ![]() and
and ![]() have a point in common. But this contradicts
Axiom 8.
have a point in common. But this contradicts
Axiom 8.
![]()
![]()