Exam Information for Math 141

As it says on the course syllabus, there are two midterms and a final in MAT141, which count for 25%, 25%, and 30% of your grade, respectively. No Make-up exams will be given. If you miss an exam due to a documented medical or family reason, that score will be replaced by the grade on the balance of the course. If you miss more than one exam for such reasons, you should probably withdraw from the course.

First Midterm: during class on Monday, October 18, 2010

The midterm covers Chapter 1, 2, and some of chapter 3 in the text.
Doing all of the homework problems prior to the exam is a very good idea. Doing additional problems from the text can be helpful.

For the exam, make sure that you know

• The precise statement of basic definitions (this is not an exhaustive list): supremum, infimum, upper- and lower-bounds, accumulation points, etc.; what it means for a sequence to converge, the limit of a function, etc.
• The statements of the major theorems: Bolzano-Weierstrauss, Intermediate Value Theorem, Extreme Value Theorem, etc.;
• how to do a proof by induction;
• how to write a careful proof that a sequence converges, or that a function has a limit, etc.
• how to calculate (but not necessarily prove) limits of sequences, sums of series, etc.
• all sorts of other important things that I might ask you but didn't think of just now.

If you wish to use a calculator on the exam you may, although it is by no means necessary and unlikely to be of any help: all problems may be readily done without one.

To give you some idea of what to expect, here is the first exam from last year. Keep in mind, however, that I didn't write this exam, so the format and choice of problems will certainly differ. In addition, their exam was a bit earlier and they hadn't yet covered any of chapter 3. Also, problem 6 uses the series definition for

e^x = 1 + x + x²/2 + x³/3! + x⁴/4! + ...,
which we didn't discuss. Still, this is better than nothing.
Here are the solutions to last year's exam. Please make a serious attempt at the exam before looking at them!

Al will be holding a review session on thursday evening at 5:30. Go to the 3rd floor of the SAC around 5:15, and he will find a nearby room. Also, I will review in class on friday.

Results: While the exam had some challenging problems (especially 5d and 2b, which were meant to be hard), I was a bit surprised at how much trouble some people had with problems 1 and 3, and also 5a. Oh well. Note that if you got a C (or even an F) on the test, you can still recover from it and do well in the course. But you will have to make some real changes.
Below is a graph of the grade distribution on the exam.

low score: 6 mean: 47 median: 41 high score: 79 possible score: 90

range letter grade 60-90 A-, A 40-59 B-, B, B+ 30-39 C, C+ 25-30 C- 15-24 D 0-14 F

You can check your grade here.

Here is a copy of the exam so you can relive the magic. Also, here are the solutions to the exam.

Second Midterm: in class on Wednesday, November 17, 2010

The second midterm will cover the material we have covered since the first exam, specifically material from chapters 3 and 4. As on the previous exam, you should expect to be asked to give some definitions or state some theorems precisely, do a proof or two, and do a few problems that are more calculational in nature.

The second midterm from last fall is available; you should be able to do all of the problems. Keep in mind, however, that we will have covered a bit more material (particularly sections 4.6 and 4.7), and some of the material on their exam was covered on our first midterm. Here are the solutions, but please attempt the problems before consulting them.

For the exam, make sure that you know

• The precise statement of basic definitions (this is not an exhaustive list): the limit of a function, what it means for a function to be strictly increasing or decreasing, the inverse of a function f, supremum and infimum of a function, a function with a removable discontinuity, the logarithm with a given base, the derivative of a function.
• The statements of the major theorems: Intermediate Value Theorem, Extreme Value Theorem, the Mean Value Theorem, Cauchy's Mean Value Theorem, L'Hospital's rule.
• The various rules and techniques for taking derivatives, including the prodcut, quotient, and chain rules; derivatives of trigonometric, inverse trigonometric, exponential, and logarithmic functions; logarithmic and implicit differentiation.
• Max/Min problems, related rates, and limits of functions (including L'hopital's rule)
• Expect a proof involving induction, and another proof of some sort.
• all sorts of other important things that I might ask you but didn't think of just now.

As on the first midterm, a calculator is allowed but almost certainly of little use.

Results: Here is the exam, and here are the solutions.

Some people did reasonably on this exam, but a few did very, very poorly. Quite a few made some disturbing mistakes, like not knowing the chain rule. These people need to focus more on fundamentals as well as the theory.
Below is a graph of the score distribution on the exam.

low score: 24 mean: 56.8 median: 55 high score: 91 possible score: 100

range letter grade 70-100 A-, A 50-69 B-, B, B+ 35-49 C, C+ 20-34 C- 10-19 D, D+ 0-9 F

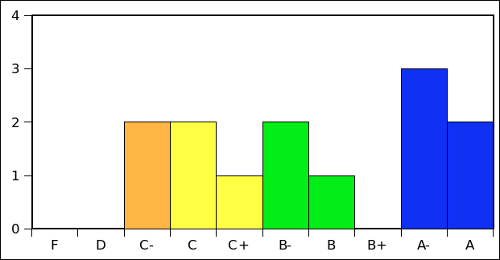
You can check your grade here.

Final Exam: 11:15am on Monday, December 13, 2010

The final will be cumulative, covering everything that we have done in the class. However, extra emphasis will be on material since the second midterm, specifically that on integration (chapter 5).

Half of the final will be MAT131-style problems. If you can do well on these, you will get at least a B in the course. If you cannot do well on these, don't expect a decent grade, no matter how many theorems you can prove.

As agreed to in class, the first half of the final will be in-class on wednesday, Dec 8. To help you get an idea of what is on a MAT131 final, here are a couple of old ones:

• final from Fall 2003, and solutions.
  On this final, problem 3 is about Newton's method, which we didn't really cover. You can safely skip this one.
  Problem 7 asks for "2 circumscribed rectangles", which means the upper sum with two intervals.
• A collection of sample problems from Fall 1998, and their solutions.
  In this collection, problem 7 asks for the "left-hand sum", "right-hand sum", and "trapezoid approximation". One of these is an upper sum, the other a lower sum, and the trapezoid approximation is their average. You should be able to figure out which is which.
  Problem 13 asks for the "second Taylor polynomial for f(x) at x=π/2". This is a quadratic polynomial p(x) = ax² + bx + c for which f(π/2) = p(π/2), f'(π/2) = p'(π/2), and f"(π/2) = p"(π/2). You should be able to figure out the problem from there. [We don't typically do this in MAT131 anymore, but you should be able to figure it out.]
• The final from spring 2009, with solutions. Sorry, I don't have a version without the solutions.

If you got at least 85 (out of 124) on part 1 of the final, you are guaranteed a grade of at least B in the course. If you got below 85, you should plan to redo another version of part 1 during the final period on monday.
There will also be a second part of the final on monday: people who got over 100 points on part 1 should only do part 2 (your grade on part 1 is sufficient), and if you got between 85 and 100, you MAY do part 1 over, but you don't have to. Indeed, I recommend that in most cases you should focus on part 2.
As mentioned, part 2 will have 4-5 definitions or statements of major theorems, a proof by induction, and 2-4 other proofs.

You can check your grade here.

Part 2 of the final