



Next: A proposed public-key system
Up: Subset-Sum (Knapsack) problems and
Previous: Subset-Sum (Knapsack) problems and
Contents
Subset-sum problems are hard
A subset of the numbers
adds up to 5842. Spend a few minutes
trying to find such a subset. Whether you succeed or not, I hope
you are convinced the task is not trivial.
This is an example of a subset-sum problem. In general,
we are given 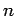 natural numbers
natural numbers 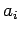 and a target number
and a target number 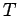 and
asked to find a
and
asked to find a
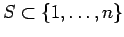 with
with
A seemingly simpler problem is the subset-sum decision
problem. For a given 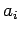 and
and 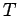 , decide whether there is an
, decide whether there is an  for which
for which 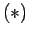 holds, without being required to identify such an
holds, without being required to identify such an  .
However, it can be proved that the decision problem is just as difficult
as the subset-sum problem in this sense:
.
However, it can be proved that the decision problem is just as difficult
as the subset-sum problem in this sense:
Theorem 17
Suppose we had a method of solving the subset-sum decision
problem. Then we could solve a subset-sum problem using the assumed
method 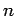 times.
times.
(the 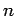 is not particularly important-- the
main thing is that the number of uses of the method is not too large.)
is not particularly important-- the
main thing is that the number of uses of the method is not too large.)
Proof: Begin by using the method to decide if
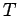 is a sum of the
is a sum of the 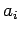 -- if not, we can stop immediately. Then
use the method to determine if
-- if not, we can stop immediately. Then
use the method to determine if 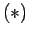 holds for some
holds for some
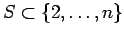 .
If the answer is yes, we ignore
.
If the answer is yes, we ignore 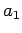 for the rest of the analysis. If
the answer is no, we know we must have
for the rest of the analysis. If
the answer is no, we know we must have 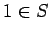 . In this second case,
we continue by using the method to decide whether there is
. In this second case,
we continue by using the method to decide whether there is
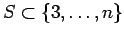 with
with
A yes answer means we can assume 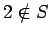 , otherwise
, otherwise 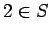 .
.
The idea of this proof is more important than
the specific result. We show that one problem is as difficult as another
by showing that a method of solving the supposedly easier problem can be
used to solve another problem. This involves constructing one or several
easier problems whose solution answers the hard problem. We saw another
example of this idea in our discussion of the Rabin encryption system
(section 3.3).
Using more elaborate versions of the techniques in
Theorem 17, it can be shown that a method of solving
the subset-sum decision problem could be used to solve many other problems,
including:
- Factoring
- The Travelling Salesman
Problem
- Any Integer Programming Problem
- The Satisfiability
Problem
Don't worry if you are not familiar with the details
of these problems. The important point is that they are all well-known
problems for which many people have been unable to find efficient solution methods, which makes it unlikely that there is a method which solves
all subset-sum decision problems efficiently (we will go into more detail
on this in section 5).
The discussion above makes it plausible that some subset-sum problems
are difficult. Further, there is some evidence that the ``typical''
subset-sum problem is not easy.
V. Chvatal3 has shown that if the 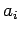 and
and 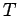 are randomly chosen, then with high probablility (i) there will be no
are randomly chosen, then with high probablility (i) there will be no
 for which
for which 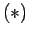 holds (ii) certain simple ways of proving this will
not work.
holds (ii) certain simple ways of proving this will
not work.
Footnotes
- ...
V. Chvatal3
- ``Hard Knapsack Problems,'' Operations Research,
vol. 28, pp 1402-1411




Next: A proposed public-key system
Up: Subset-Sum (Knapsack) problems and
Previous: Subset-Sum (Knapsack) problems and
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() natural numbers
natural numbers ![]() and a target number
and a target number ![]() and
asked to find a
and
asked to find a
![]() with
with 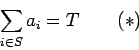
![]() is a sum of the
is a sum of the ![]() -- if not, we can stop immediately. Then
use the method to determine if
-- if not, we can stop immediately. Then
use the method to determine if ![]() holds for some
holds for some
![]() .
If the answer is yes, we ignore
.
If the answer is yes, we ignore ![]() for the rest of the analysis. If
the answer is no, we know we must have
for the rest of the analysis. If
the answer is no, we know we must have ![]() . In this second case,
we continue by using the method to decide whether there is
. In this second case,
we continue by using the method to decide whether there is
![]() with
with 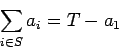
![]() and
and ![]() are randomly chosen, then with high probablility (i) there will be no
are randomly chosen, then with high probablility (i) there will be no
![]() for which
for which ![]() holds (ii) certain simple ways of proving this will
not work.
holds (ii) certain simple ways of proving this will
not work.