



Next: Subset-Sum (Knapsack) problems and
Up: Encryption techniques based on
Previous: The Rivest-Shamir-Adleman public key
Contents
Subsections
A public key system as hard as factoring
It is possible in theory that there is some way of computing 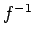 for the system in the previous section that does not involve determining
for the system in the previous section that does not involve determining  and
and 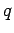 . In the original RSA paper, the authors say
. In the original RSA paper, the authors say
It may be possible to prove that any general method
of breaking our scheme yields an efficient factoring algorithm. This
would establish that any way of breaking our scheme must be as difficult as factoring. We have not been able to prove this conjecture,
however.
To see the difficulties involved in trying to prove such a thing,
suppose that one could show that knowledge of a ciphertext  and a plaintext
and a plaintext 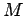 enabled one to find
enabled one to find  and
and 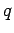 . Then one
could factor
. Then one
could factor 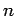 as follows:
as follows:
- Choose any
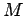 .
.
- Compute
 . [Remember, we are assuming
. [Remember, we are assuming
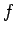 is publicly available. Furthermore,
is publicly available. Furthermore,  can't be too hard
to compute, or the code would be impractical.]
can't be too hard
to compute, or the code would be impractical.]
- Use the assumed
method to obtain
 ,
, 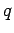 .
.
In words, we are unable to distinguish between the situation
in which  is obtained from
is obtained from 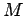 (easy) and the (presumably difficult)
situation in which
(easy) and the (presumably difficult)
situation in which 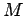 is obtained from
is obtained from  .
.
Rabin has suggested an alternative to the RSA system in which there
is a direct connection to factoring. As in RSA, 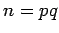 is announced
publicly, with primes
is announced
publicly, with primes  ,
, 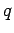 kept secret. For technical reasons, we
assume
kept secret. For technical reasons, we
assume
 .
The encoding function is
.
The encoding function is
The way we avoid the difficulty described above is that there are
four numbers
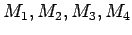 with
with
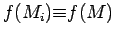 . The
key facts are:
. The
key facts are:
- If
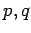 are known, it is easy
to compute all the
are known, it is easy
to compute all the 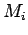 given
given  .
.
- If we are given
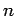 ,
,  ,
and all the
,
and all the 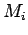 , we can calculate
, we can calculate  ,
, 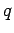 .
.
We are not able to obtain  ,
, 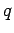 from just one
of the
from just one
of the 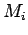 , so the approach based on
, so the approach based on 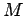 and
and  described above
won't work. One drawback of this system is that, even with knowledge of
described above
won't work. One drawback of this system is that, even with knowledge of
 and
and 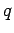 , one can only say the number sent is one of the four
, one can only say the number sent is one of the four 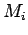 ,
without being able to identify which one. In practice, this is not
serious, since it is very unlikely that more than one of the
,
without being able to identify which one. In practice, this is not
serious, since it is very unlikely that more than one of the 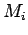 would
correspond to a feasible message.
would
correspond to a feasible message.
proof of 1: Since
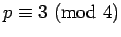 , there is an integer
, there is an integer 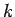 with
with 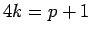 .
If
.
If
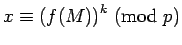 , then using Corollary 8:
, then using Corollary 8:
Similarly if
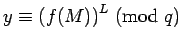 [
[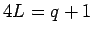 ], then
], then
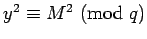 .
The
.
The 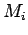 are given from Corollary 4 by
are given from Corollary 4 by
proof of 2: If we know the 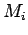 , there will be two like
, there will be two like  and
and 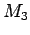 above with
above with
 and
and
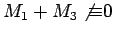 mod
mod 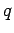 .
Thus we can calculate
.
Thus we can calculate 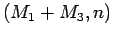 to obtain
to obtain  .
.
One problem with this system is that a person with access to a
``black box'' that computes 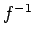 could quickly discover
could quickly discover 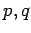 ,
even if we assume that the person trying to break the code gets
only one of the
,
even if we assume that the person trying to break the code gets
only one of the 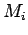 , chosen randomly. The attacker keeps generating
pairs
, chosen randomly. The attacker keeps generating
pairs 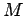 ,
,  until he gets an
until he gets an 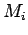 with
with 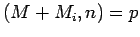 or
or 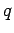 .
.
In the previous section, we assumed the primes were of the form 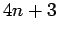 in order to make the square root calculation as easy as possible. However,
square roots can be efficiently calculated for any prime.
in order to make the square root calculation as easy as possible. However,
square roots can be efficiently calculated for any prime.
Let 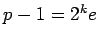 , where
, where 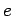 is odd. Define the sets
is odd. Define the sets
If  is a square, it must be in
is a square, it must be in 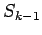 .
Thus the sets
.
Thus the sets 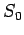 and
and 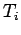 ,
, 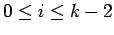 partition the squares.
Furthermore, by starting with
partition the squares.
Furthermore, by starting with 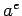 and squaring, it is possible to
identify which member of the partition includes
and squaring, it is possible to
identify which member of the partition includes  .
.
If 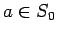 ,
,
so
it is easy to calculate a square root of  . (when
. (when 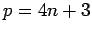 , all
, all 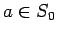 )
)
Let 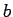 be a non-square mod
be a non-square mod  .
Since
.
Since
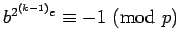 for all
non-squares, it is easy to find one.
for all
non-squares, it is easy to find one.
We argue by induction on 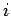 that square roots can be efficiently
calculated for
that square roots can be efficiently
calculated for 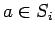 . We have seen that this is the case for
. We have seen that this is the case for 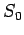 .
If
.
If
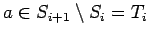 , there is an even
, there is an even 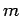 with
with
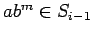 . Specifically, if
. Specifically, if 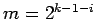 ,
,
Since 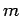 is even, division of a square root of
is even, division of a square root of  by
by 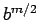 gives a square root of
gives a square root of  .
.




Next: Subset-Sum (Knapsack) problems and
Up: Encryption techniques based on
Previous: The Rivest-Shamir-Adleman public key
Contents
Translated from LaTeX by Scott Sutherland
2002-12-14
![]() is announced
publicly, with primes
is announced
publicly, with primes ![]() ,
, ![]() kept secret. For technical reasons, we
assume
kept secret. For technical reasons, we
assume
![]() .
The encoding function is
.
The encoding function is ![]() , there is an integer
, there is an integer ![]() with
with ![]() .
If
.
If
![]() , then using Corollary 8:
, then using Corollary 8:
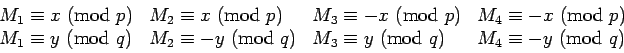
![]() , there will be two like
, there will be two like ![]() and
and ![]() above with
above with
![]() and
and
![]() mod
mod ![]() .
Thus we can calculate
.
Thus we can calculate ![]() to obtain
to obtain ![]() .
.
![]() could quickly discover
could quickly discover ![]() ,
even if we assume that the person trying to break the code gets
only one of the
,
even if we assume that the person trying to break the code gets
only one of the ![]() , chosen randomly. The attacker keeps generating
pairs
, chosen randomly. The attacker keeps generating
pairs ![]() ,
, ![]() until he gets an
until he gets an ![]() with
with ![]() or
or ![]() .
.
![]() , where
, where ![]() is odd. Define the sets
is odd. Define the sets
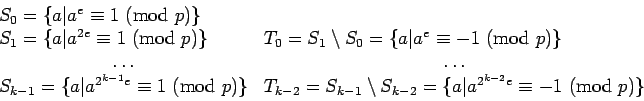
![]() ,
,
![]() be a non-square mod
be a non-square mod ![]() .
Since
.
Since
![]() for all
non-squares, it is easy to find one.
for all
non-squares, it is easy to find one.
![]() that square roots can be efficiently
calculated for
that square roots can be efficiently
calculated for ![]() . We have seen that this is the case for
. We have seen that this is the case for ![]() .
If
.
If
![]() , there is an even
, there is an even ![]() with
with
![]() . Specifically, if
. Specifically, if ![]() ,
,