A proposed public-key system based on subset-sum

As an example of an easy subset sum problem, consider the task of determining what subset of

$$\begin{array}{*{10}{r}}1&3&6&14&27&60&150&300&650&1400 \end{array}$$ (1)

adds up to 836. The $a_i$ in this problem have the special property that every number is greater than the sum of all preceding numbers ($27>1+3+6+14$, etc). [A sequence with this property is called super-increasing.]

1400 clearly cannot be in the set. If 650 is not in the set, we would be in trouble, since the sum of the remaining numbers is $<650$, hence $<836$. Thus 650 must be in the set, and we now have the task of finding numbers which add up to $836-650 =186$. 300 is too big, and the same reasoning as before shows that 150 must be in the set. If we continue, it is easy to identify the desired set as $\{650,150,27,6,3\}$.

We began section 4.1 with the problem of identifying a subset of

$$\begin{array}{*{10}{r}}267&493&869&961&1000&1153& 1246&1598&1766&1922\end{array}$$

which adds up to 5842. What we didn't mention before was that the $a_i$ were carefully chosen to make them directly related to the $a_i$ in the easy subset-sum problem (1):

$${267}\equiv{300(1000)}\hbox{ (mod }{2039})\quad{493}\equiv{27(1000)}\hbox{ (mod }{2039})\quad 869{\equiv}60(1000)$$

and so forth, where 2039 is a modulus chosen in advance (larger than any of the numbers in the easy subset-sum problem) and 1000 is an arbitrarily chosen number. (we must have $\gcd(2039, 1000)=1$)

To find the subset, begin by solving ${1000U}\equiv{1}\hbox{ (mod }{2039})$, which gives $U=1307$. If we let $b_i$ be the numbers in the easy problem, the hard problem can be written as

$${\sum_{i\in S}(1000b_i)}\equiv{5842}\hbox{ (mod }{2039})$$

When we multiply by 1307, this becomes

$$\sum b_i{\equiv}1307(5842){\equiv} 1478$$

It is easy to identify $\{1400,60,14,3,1\}$ as a subset which adds to 1478, and the desired subset of the original system is

$$\{{1246}\equiv{1400(1000)}\hbox{ (mod }{2039}),869{\equiv}60(1000),1766, 961,1000\}$$

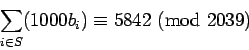
This would seem to give us a good public-key system: a problem which is easy once some special information (the 2039 and the 1000) is known, difficult without the information. Unfortunately, the special type of subset-sum problem created in this way can be solved even without the special information. There is a sequence of papers showing how to solve special subset-sum problems and proposing a refinement which, in turn, was solved by the next paper in the sequence. This has not happened with the RSA system, but there is no guarantee that it won't!