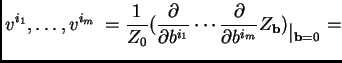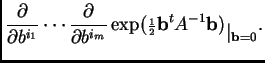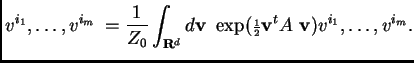
The ![]() -point functions are a step towards the ultimate aim of our calculation.
They enter at this moment because they can be calculated
by repeated differentiation of
-point functions are a step towards the ultimate aim of our calculation.
They enter at this moment because they can be calculated
by repeated differentiation of ![]() .
.
For example, note that
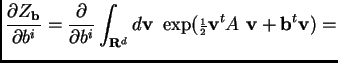
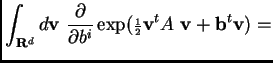
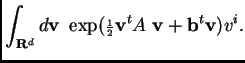
So the 1-point function ![]() is given by
is given by
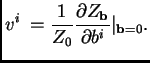
Similarly the ![]() -point function
-point function
![]() is given by
is given by