tidesII-3

Fourier Analysis of Ocean Tides II

3. The complete calculation

The method followed in the sample problem can be extended to the complete calculation. Given the tidal record H(t) over a suffuciently long time interval [0,P],

A₀ is the average value of H(t) over the interval [0,P].
A₁ is the average value of H(t)cos(v₁t) over the interval [0,P].
B₁ is the average value of H(t)sin(v₁t) over the interval [0,P].
A₂ is the average value of H(t)cos(v₂t) over the interval [0,P].
etc.

How were these calculations made? In terms of calculus, the average value of H(t)sin(v_kt) over the interval [0,P] is (1/P) times the integral from 0 to P of H(t)sin(v_kt)dt. With a modern computer a computation like this is not a problem, once H(t) has been presented as a file the computer can read. In the nineteenth and early twentieth century other methods were needed. One method, partially explained in Schureman, is the use of stencils overlaid on the hourly records for H(t) (regularly tabulated in columns) so that the terms with a common trigonometric factor would appear in a linked series of windows. The amount of calculation is still substantial, and must be completely repeated for each port.

Kelvin's Harmonic Analyser. Kelvin devised a mechanism for implementing this calculation.

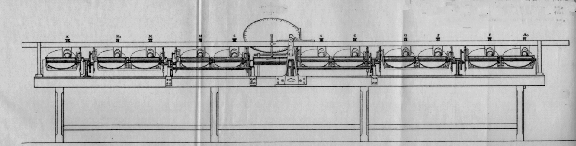
Kelvin's Harmonic Analyser. From Kelvin (=Sir William Thomson, Baron Kelvin), The tidal gauge, tidal harmonic analyser, and tide predicter, in Kelvin, Mathematical and Physical Papers (Volume VI), Cambridge 1911, pp 272-305. [From the Minutes of the Proceedings of the Institution of Civil Engineers, March 11, 1882.]

This machine is designed to compute the eleven coefficients A₀, A₁, B₁, ... A₅, B₅. The tidal record is diplayed on the horizontal drum in the center of the picture. The drum is linked by gearing to the eleven disks, part of eleven disk-sphere-cylinder integrators. If the drum advances t units, the leftmost disk rotates t radians, the next two disks rotate sin (v₁t)/v₁ and -cos(v₁t)v₁ radians, respectively, the third and fourth disks rotate sin (v₂t)/v₂ and -cos(v₂t)/v₂ radians, respectively, etc. As the drum turns, the vertical pointer tracks the height of H(t). The eleven integrator spheres move in unison with the pointer. At the end, the total distance rolled by each cylinder will record one of the eleven desired integrals. Dividing by the length of the record yields the corresponding coefficient. Presumably the gearing could be changed to compute the next five pairs of coefficients. This mechanism is no longer in existence, and it is not clear to me whether or how it was ever used, but a smaller one, with five integrators, is in the South Kensington Museum.