Suppose we now look at a cell in a layout. Draw the circumscribing circle as well, or at least its intersection with the cell. Where it extends beyond the cell, the line cut off by the cell boundary will be the bisector of the rhombus associated to two discs whose hexagonally circumscribed circles intersect.

We can now divide up the cell into distinct regions of three types:

The points in the cell which do not belong to the enlarged disc	The points in the cell lying in a rhombus associated to a neighbouring cell.	The parts of the circumscribing disc not belonging to one of these rhomboi.

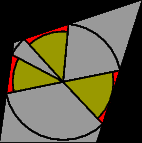
The density of the distribution in the first type of region is of course 0, since by definition such a region contains no part of a disc. The density of the distribution in the third type is just the ratio of the radius of the disc to that of the larger one. Both densities are strictly less than the density of the disc in its regular circumscribed hexagon. The crux of the argument is now to examine regions of the second type.