What is meant by the density of a layout of discs in the plane? Density is measured by the fraction of area covered by the discs.

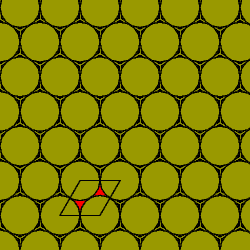
For example, the density of the layout on the left below is the ratio of the area of a circle to the square which just encloses it, and the density of the layout on the right is the ratio of the area of a circle to that of its circumscribing regular hexagon. It is visibly apparent, and easy to calculate explicitly, that the density on the right is greater. It is also easy to prove that any lattice packing (i.e. a packing in which the discs are located on an arithmetic lattice) has density at most that of the hexagonal packing, as the figures illustrate. The density of a lattice packing is the ratio of the area of a disc to that of a fundamental parallelogram, and among all lattice packings with a given size disc the hexagonal lattice clearly minimizes the area of a suitable fundamental parallelogram. This was observed first by Gauss.

The fundamental parallelogram of this lattice is a square, and the density of the distribution of discs is the ratio of the area of a circle to its circumscribing square.	The base of the fundamental parallelogram is necessarily the same, but its height is the smallest possible among lattice distributions of the disc. The density is therefore maximal among such distributions.

The statement of Thue's Theorem is a bit subtle, because the notion of density for an infinite layout, other than one associated to a lattice, is a bit subtle. Instead of trying to define exactly what we mean by the density of an arbitrary infinite layout, we shall just apply one intuitive principle which must follow from any valid definition.

Suppose we are given a distribution of non-overlapping discs on the plane, and suppose that the plane is partitioned into regions (not necessarily of finite area) surrounding each disc. For each one, calculate the ratio of the area of the disc to the area of the region. This is the the density of the distribution in that region. Then, no matter what the partition is, the density of the overall distribution cannot be greater than than the maximum of its densities in the various regions.

The density of the distribution cannot be greater than the maximum density among the smaller regions.

Now we shall associate to any distribution of equal-sized discs in the plane a partition of the plane into regions, with one disc in each region. We shall prove that the proportion of disc in each of those regions can be no more than the density of the hexagonal packing. This will show that no distribution will be denser than the hexagonal packing, which is Thue's theorem.