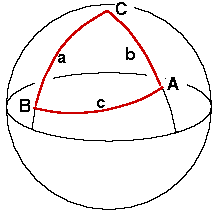
Starting point and destination, together with the North Pole, form a spherical triangle.

The points A and B form a spherical triangle with the North Pole C. Each side of this triangle is an arc of a circle centered at the center of the earth, i.e. a great circle. The length of a great-circle arc can be read off immediately from the corresponding central angle: the measurement of the central angle in minutes of arc gives the length of the arc in nautical miles. If we call a, b, c the sides opposite vertices A, B, C, then in this triangle we know a, b, and C. Side a has length 90o minus the latitude of vertex B, and vice-versa. The angle C is the difference between the longitudes of A and B. This is enough information to solve for all the elements of the triangle, in particular side c (the great-circle distance) and angle A (the initial course).

Here is the problem from Dutton:
We may solve for c using the spherical law of cosines:
This gives c = 74.36o or 4461.6 nautical miles.
Once c is known, A can be calculated using the spherical law of sines:
Using the known values for a, c, and C this gives A = 57.77o, or 57o46'19".