kepler2

$e-MATH$

Celestial Mechanics on a Graphing Calculator

2. Euler's method

For the restricted 2-body problem, some important simplifications can be introduced in the equations expressing Newton's laws.

The larger body may be assumed to remain at rest, and its position may then be chosen as the origin of the coordinate system. So in the equations we may take x' = 0.
The motion of the smaller body must lie in the plane determined by its initial velocity direction and the position of the larger body. So the system is only 2-dimensional. For obvious reasons we exclude the case in which the initial velocity vector points exactly at the larger body.
Finally, we can rescale the space and time coordinates to make the constant Gm' equal to 1. For example, to interpret these calculations in terms of the motion, in our solar system, of a planet at approximately one earth-orbit radius, the unit of length would correspond to 7.2x10¹⁰m (approximately 45 million miles), and the unit of time to 1.7x10⁶ seconds, approximately 19 days.

We are left with the following system of differential equations, where x and y are the components of the position vector x of the smaller body, and v,w are the corresponding components of its velocity vector v. Note that d, the distance between the two bodies, is now (x²+y²)^1/2.

dx -- = v dt	dv -x -- = --------- dt (x²+y²)^3/2
dy -- = w dt	dw -y -- = --------- dt (x²+y²)^3/2

Euler's method (Leonhard Euler, 1707-1783) is the most elementary numerical way of attacking a system of differential equations. The algorithm takes as input the equations, the length of time T over which a solution is to be approximated, the number n of steps desired for the approximation, and initial values x₀, y₀, v₀, w₀ for the four unknown functions.

The method consists in iterating n times the following calculation, starting with i = 0; dt is the time increment T/n.

x_i+1 = x_i + v_i dt	-x_i v_i+1 = v_i + --------- dt (x_i²+y_i²)^3/2
y_i+1 = y_i + w_idt	-y_i w_i+1 = w_i + --------- dt (x_i²+y_i²)^3/2

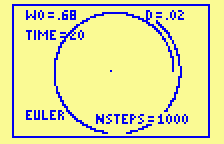
Unfortunately, while in theory Euler's method can give any desired accuracy provided the number of steps is big enough, that number of steps can be impractically large. For example, here is what happens when one applies Euler's method on a TI-82 graphing calculator to the restricted 2-body problem, as given above, with x₀=2, y₀=0, v₀=0, w₀=.68, T=20 and n=1000.

The ellipse does not close up. Doubling the number of steps takes twice as long but still does not give a closed image.