Alberti's Perspective Construction

4. The backwards construction

In Della Pittura Alberti criticizes a rival construction because it does not locate the position of the eye. In fact, if the pavement construction has been done properly, it can be run backwards to locate the ideal viewing position for the picture: the point in space from which the illusion should be most perfect. The easiest way to show how this works is by an extension of our original checkerboard construction. This image may be JAVA animated by clicking on its surface.

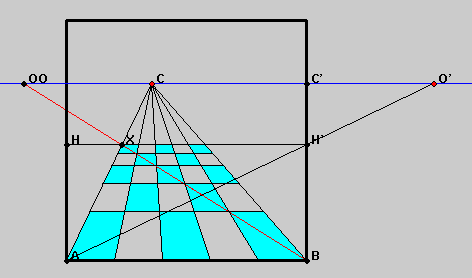
If the diagonal through B is extended beyond the image X of the far left corner of the checkerboard, it meets the horizon in the point OO. (Any one of the parallel diagonals will pass through OO). Arguing with similar triangles, we can show that the distance from OO to C is equal to the distance from O' to C' and is therefore equal to the distance from the picture of the eye used in the construction.

The argument runs as follows: Equating ratos of corresponding sides in the similar triangles H' C' O' and H' B A gives

|H' C'| / |B H'| = |O' C'| / |A B|.

In the similar triangles X C OO and X A B the ratios of the altitudes must be the same as the ratio of the bases. This gives

|H' C'| / |B H'| = |OO C| / |A B|.

It follows that |OO C| = |O'C'|.