Alberti's Perspective Construction

This column is an elaboration, with animations, of the geometry contained in my review of The Invention of Infinity by J. V. Field (Oxford, 1997); the review appeared in the Notices of the A.M.S. and is available online. For cultural background and a much more detailed look at the history please consult Field's book or The Heritage of Giotto's Geometry by Samuel Y. Edgerton, Jr. (Cornell, 1991). Alberti's Della Pittura is available online in an English translation, in the visual arts ``Notebook''. The relevant part of the text is in the second webpage devoted to Book I. An excellent web resource with many useful links is the Perspective & Pictures page at the University of Newcastle, Australia.

1. One-point perspective

One-point perspective is the most common systematic method for representing space on a surface. The idea is that the picture in its frame should give the illusion of being a window through which the immobile eye of the observer looks at an outside 3-dimensional world. (Alberti speaks of the canvas as ``an open window through which I see what I want to paint.'') Each spot visible through the window gives a spot in the picture, located at the intersection with the picture plane of the straight line joining it to the eye. Albrecht Dürer illustrates this method in a famous 1525 engraving: a hook on the wall is the eye, and a taut string is the straight line joining the eye to a visible spot beyond the frame.

All the elements of one-point perspective are concretely realized in this engraving by Albrecht Dürer. The paper on which the picture is to be drawn swings out of the way. The string, kept taut by a weight, is led from the hook (the eye of the ideal observer) to a point on the object being portrayed. Presumably a vertical and a horizontal thread are slid so as to record the point at which the string crosses the picture plane. Then the string is relaxed, the drawing swings back, and that point is marked on the paper. This image (itself drawn in one-point perspective) gives a visual explanation of the principle and should not, I believe, be interpreted as a snapshot of an actual procedure.

An important feature of one-point perspective is the vanishing point:

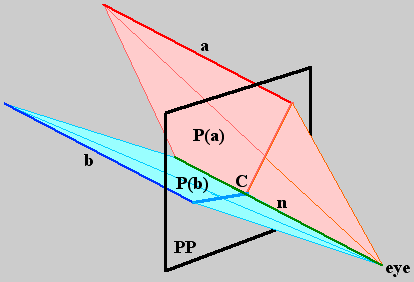All lines in space which are perpendicular to the picture-plane appear in the picture as emanating from a single point (``the point at infinity'' or ``the vanishing point''), which is the the foot of the perpendicular from the eye to the picture-plane.

The proof, sketched here, is an argument in solid geometry: By the construction, any straight line a in space appears as a straight line in the picture (the intersection of the picture-plane PP with the plane P(a) determined by a and the eye). If a is perpendicular to PP, then at any intersection point x of P(a) with PP the line through x in P(a) parallel to a will also be perpendicular to PP. If b is another line in space, then P(a) and P(b) intersect (they both contain the eye). Their intersection will be a line n. If b is also perpendicular to PP, then a and b are parallel, and so both are parallel to n. So n is a line through the eye which meets PP perpendicularly, in a point C. Since C belongs to PP, P(a) and P(b), the lines in the picture corresponding to a and b must intersect in C: C is the vanishing point.

It is said that the ancients knew one-point perspective and that it was ``rediscovered'' in the Renaissance. Alberti addresses this point explicitly: ``How difficult this is can be seen in the works of antique sculptors and painters; ... it was hidden and unknown to them.'' In fact, in the works from Roman times that I have examined, where the artists were using linear perspective to create the illusion of depth, there is no global vanishing point. As a consequence the images grow more unlikely the closer they are studied, sometimes ending up with impossible, Escher-like configurations, as remarked in Michael Gunther's website Roman Painting: Frescoes from Campania (see in particular Theatrical Scenery and III Style Decoration; see also the cityscape from Boscoreale on the Odyssey website (the room it decorates is in the Metropolitan Museum) and the sumptuous but geometrically perplexing mural from John Hauser's ``Pictures of History - Pompeii.'')

There is more to one-point perspective than the vanishing point. The most delicate question is the following: given a series of equally spaced points along a line perpendicular to the picture-plane, how will their images be spaced along the corresponding straight line in the picture? The answer is straightforward to calculate numerically but for an artist it would be very awkward to have to reckon all the distances and measure them off, one by one, in the picture.

In this column we will investigate a geometric algorithm for generating these lengths. The method was invented in Florence at the beginning of the 15th century, probably by Filippo Brunelleschi. It was written up by Leon Battista Alberti in 1435-36; the simplified version, described by Piero della Francesca around 1480, will be the focus of our attention.

--Tony Phillips
Stony Brook