Through Mazes to Mathematics

This page has been translated into Polish.
This page has been translated into Romanian.
This page has been translated into Spanish.

How did I get interested in counting mazes?

A Tale of Serendipidities


1982

My first encounter with these mazes was around 1982, when the labyrinthologist Jean-Louis Bourgeois showed me the maze game. He told me this game is widespread in the folk cultures of Asia; it is extremely old, since this very same design occurs on Cretan coins of the 4th-5th century BC, where it symbolizes the Labyrinth in which the Minotaur was kept. (In fact, there are much earlier examples). The legend has it that Theseus found his way out of the Labyrinth by following a thread he had unwound from a spool given to him by his sweetheart Ariadne, and so a line drawn so as to trace the path through a maze like this is often called "Ariadne's thread."

A short time later I was visiting the house of David Gay, a mathematician at the University of Arizona in Tucson. Hanging on the wall was a flat basket, about 18 inches in diameter, woven with a design that turned out to be topologically identical to the Cretan maze. David told me that this basket design is traditional with the Tohono Oʼodham (formerly "Papago") Indians, a tribe living now in northern Arizona, and that the twists and turns of the path through the maze represent events and trials in the life of the hero Iitoi shown at the entrance.

1983

Finally, a few months later, visiting my parents in Florida, and leafing through a Sotheby's catalogue, I was struck by the photograph of a page from a medieval Hebrew manuscript (a Sefer Haftorot) which was to be sold on June 23, 1983. The photograph showed this design:


Maze from a medieval Sefer Haftorot.
Click for a larger image.
Click for a much larger image.

The seven concentric walls symbolize the seven walls of Jericho. The words of Psalm 104, vv. 1-18, 20, 21 wind along the path. In the center is written "Jericho" and "The image of the wall of Jericho. The reader is as if walking." (Thanks to Prof. Robert Goldberger for the translation.) Photograph courtesy of Sotheby's Inc., New York.

Although this maze has a superficial resemblance to the Cretan maze, a close comparison shows they are quite different. The Jericho maze has 7 levels, whereas the Cretan maze has 8, and the sequence in which the levels are reached is quite different from one maze to the other. In both mazes the path goes directly to level 3 (counting the outside as 0) but in the Cretan maze it then doubles back through levels 2 and 1, whereas in the Jericho maze it continues on through levels 4 and 5 before returning to 2 and 1. The complete level sequences are 

             Cretan  0 3 2 1 4 7 6 5 8

            Jericho  0 3 4 5 2 1 6 7.

These can be interpreted as musical phrases, letting 0 = C, 1 = D, etc. The ear detects immediately that in the Cretan tune, the initial phrase is repeated in a higher pitch; as I later understood, this maze can be decomposed into the product or stacking of two copies of the four-level maze 03214.

Having seen two similar but distinct examples, I began to wonder how many more there might be. The first thing was to understand exactly what they had in common. It turns out that there are three characteristics that they share, and that define a class of mazes that can be investigated mathematically: these are the simple, alternating, transit mazes. I became interested in the problem of determining $M_n$, the number of distinct s.a.t. mazes with $n$ levels.

1985-86

By that time I was spending a sabbatical in Italy, where Michele Emmer, a professor at the University of Rome, happened to be making one of his Math/Art films, on the subject of mazes. He invited me to appear in the film and talk about s.a.t. mazes, so I wrote a script for myself which is the basis of this text. In the script I explained how you find out which permutations of integers can be level sequences of s.a.t. mazes. (This got left out of the movie.)

1986

In December of 1986 I ran into Paul Erdös at a party and told him about my interest in this combinatorial phenomenon. He asked me whether the number $M_n$ of $n$-level mazes seemed to be increasing exponentially or even factorially with $n$. This short conversation led me to think about the behavior of the function $M_n$. I was able to write him a week later that the number $I_n$ of interesting mazes increases at least exponentially with $n$. The proof showed by construction that $I_{n+4} > 6 I_n$; the 6 can be improved to 8 as follows: for each interesting maze of even depth $n$, the eight $(n+4)$-level mazes shown here


Each interesting $n$-level maze gives rise to 8 different interesting mazes of depth $n+4$; in b,g,h the path runs through the $n$-level maze backwards.

are all interesting, and these new mazes are all distinct. In this figure, the mazes are represented by their maze-paths in rectangular form. Note that the original $n$-level maze occurs both with its entrance on the right and on the left. The proof that these mazes are all distinct requires the hypothesis "interesting."

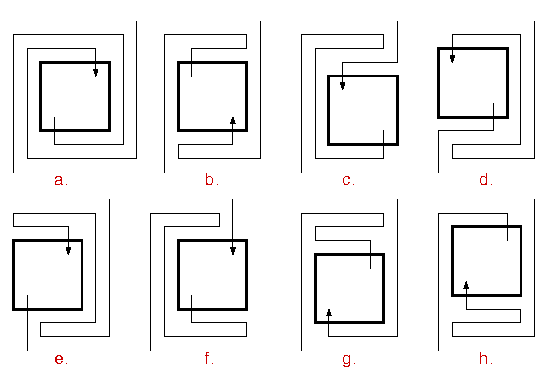
I then began to search for a way of computing $M_n$. The method I had been using was not practical for larger values of $n$, since it involved looking at a number of pairs of permutations that increased, roughly, like $((n/2)!)^2$. To compute $M_{20}$, for example, would require examination of about $10^{13}$ pairs, which would take a long time even on a very fast computer. Help arrived from an unexpected source.

1987

In the New York Times Science section for Tuesday, January 27, 1987 was an article by James Gleick about the mathematician Neil J. A. Sloane, which began: "Without quite meaning to, Neil J. A. Sloane has become the world's clearing-house for number sequences. He keeps track of easy ones, like 1, 2, 4, 8, 16, 32 ..., the powers of two. He keeps track of hard ones, like 1, 1, 2, 5, 14, 38, 120, 353 ..., the number of different ways of folding ever-longer strips of postage stamps. ... "

This was the first I had ever heard of the stamp-folding problem, but it is clearly related to the problem of counting mazes. In fact each maze of depth $n$ gives a way of folding a strip of $n+1$ stamps: put the maze in rectangular form and lay the stamps along the maze-path, one on each level (including 0 and $n$), ignoring the vertical segments. But there is a difference: the first and last stamps of a folded strip may have their free edges embedded in the interior of the packet, while the first level (after 0) and the last level (before $n$) of a maze-path must have their free ends on the outside. So if $F_n$ is the number of ways of folding a strip of $n$ stamps, we can only conclude that $M_n < F_{n+1}$.

The calculation of $F_n$ was done by John E. Koehler, S. J. for $n\leq 16$ in an article published in 1968. The numbers start as above and go up to $F_{16} = 4215768$. But what was most useful was that Koehler described a way of counting foldings of a strip of $n$ stamps ($n$ even) by looking at pairs of "$n$-patterns;" and the number of distinct $n$-patterns was available in closed form, for $n$ even: it was the $(n/2)$-th Catalan number $\mbox{Cat}(n/2)$. S.a.t. mazes with $n$ levels admit a similar enumeration; in this case the two $n$-patterns must satisfy the additional condition that guarantees a single path threading the entire maze. Now the Catalan numbers, even though they are defined with factorials, only grow exponentially; in fact $$ \mbox{Cat}(k) \sim 4^k k^{-3/2} \pi^{-1/2}$$ for $k$ large, an easy consequence of Stirling's formula. It follows that since every $n$-level maze corresponds to a pair of $n$-patterns, the number $M_n$ of $n$-level mazes ($n$ even) is $< \mbox{Cat}(n/2)^2$, and so grows at most exponentially.

More practically, there are many fewer pairs of $n$-patterns than pairs of permutations of $n/2$ elements, and Koehler's identification allowed me to compute $M_n$ through $n=22$ for $n$ even, by checking all pairs of $n$-patterns for the single-cycle property. Of course the calculation time still increases exponentially with $n$. For $n = 22$ the number of pairs of $n$-patterns to be examined was $\mbox{Cat}(11)^2 = 3455793796$. This took some 73 hours on a Sun-3 computer. The $n = 24$ calculation would take roughly 16 times as long, etc.

Jim Reeds of Bell Labs found a better method and was able to extend the calculation to $n = 28$.

One by-product of my study of these maze patterns was the realization that the maze-makers of ancient times worked by combining a limited number of fundamental forms. This allowed me to suggest how partially destroyed Roman mosaic mazes should be restored, and to detect some examples of faulty restoration in those already repaired. See The topology of Roman mosaic mazes.

Return to Main Maze Page

Return to Tony's Home Page

Tony Phillips
Math Dept SUNY Stony Brook
tony at math.stonybrook.edu
February 12 1999, May 14 2001, December 6 2007
Last edited August 11 2023