Through Mazes to Mathematics

This page in Polish
This page in Georgian

A Combinatorial Problem:
How many different n-level mazes are there?


Among the classical and medieval maze-types there are examples of different simple alternating transit mazes with the same number of levels. For instance

these three 12-level maze-paths all occur. This raises the question: How many different mazes are there with n levels?

Now it is possible to list all of the possible s.a.t. mazes of a given depth n, by looking at all the permutations of 0,...,n and discarding those which do not meet the three conditions which guarantee that a sequence corresponds to a maze. In fact, since odds and evens cannot mix in the permutation, and since 0 and n must stay fixed, it is enough to look at all pairs of permutations, one of the odd integers 1,...,n-1 (assuming n even), and one of the even integers 2,...,n-2. For example, to construct all possible 8-level mazes, one must consider pairs of permutations of 1,3,5,7 and of 2,4,6. There are 24 x 6 = 144 such pairs, so this can easily be done by hand. Here is what one finds for depths 1 through 8. In this list, the non-"interesting" mazes (those can be constructed from shallower mazes by adding trivial levels at the top and/or bottom) have been omitted. This figure shows the nuclei and rectangular mazepaths of these mazes; only one representative of each dual pair is drawn. See From rectangular path to nucleus for how these forms are related (added 3/14/2024).


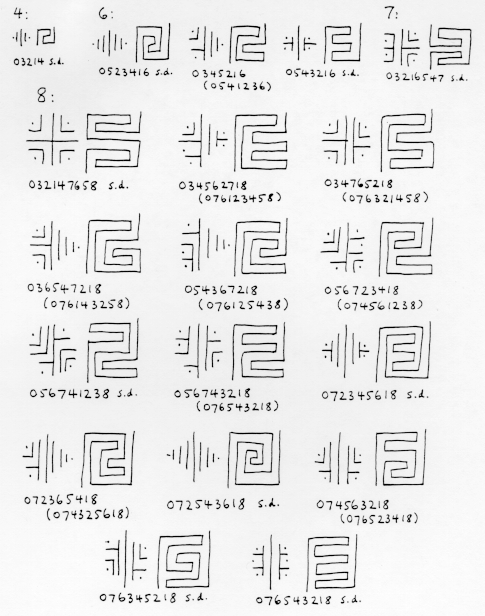
The interesting mazes of 4,6,7 and 8 levels. Only one representative of each dual pair is drawn.
s.d. : self-dual.

Corrections (03/02/2024, 03/09/2024, 03/14/2024). In "The interesting mazes of 4,6,7 and 8 levels," 034562718 should be 034567218, and the dual of 056743218 is 076541238; also the nucleus for 056723418 is wrong: its right side should be the same as the right side of 072345618 or 034562718. Thanks to Dani Novak.

Here are the data in tabular form: 


Depth   Number of mazes    Interesting mazes

  1              1                 none

  2              1                 none

  3              1                 none

  4              2                03214

  5              3                 none

  6              8          0523416   0543216
                            0345216   0541236

  7             14               03216547 

  8             42   032147658   034567218   034765218 
                     036547218   054367218   056723418 
                     056741238   056743218   072345618  
                     072365418   072543618   074325618 
                     074561238   074563218   076123458 
                     076125438   076143258   076321458 
                     076345218   076523418   076541238 
                     076543218

For depth 9 one would have to consider 24 x 24 = 576 permutations, and the possibilities of error increase. The following numbers were calculated using computers. 

                    n           M(n)        I(n)
                    1             1          0 
                    2             1          0 
                    3             1          0 
                    4             2          1
                    5             3          0 
                    6             8          4 
                    7            14          1 
                    8            42         22 
                    9            81         11   
                   10           262        142  
                   11           538         95  
                   12          1828       1014 
                   13          3926        808   
                   14         13820       7796
                   15         30694       6980    
                   16        110954      63386    
                   17        252939      61725   
                   18        933458     538534  
                   19       2172830     558853    
                   20       8152860    4740658    
                   21      19304190    5171300    
                   22      73424650   42969130

                   24     678390116

                   26    6405031050 

                   28   61606881612 

                   30  602188541928

                   32 5969806669034
Here M(n) and I(n) are the numbers of mazes and of interesting mazes of depth n. The values for 24, 26 and 28 were obtained by Jim Reeds of Bell Labs by a method which does not seem to apply to odd depth-numbers. The values for 30 and 32 are reported in Lando and Zvonkin's 1993 paper as due to V. R. Pratt.

The interesting 9-level mazes are shown this figure by their rectangular maze-paths; again, only one representative of each dual pair is drawn.


The 11 interesting mazes of depth 9.

The next figure shows the maze paths of the 5 self-dual very-interesting mazes of depth 10; these are mazes which also have no internal sequences of trivial levels.


The 5 very-interesting self-dual mazes of depth 10. The patterns labelled alpha_10 and gamma_10 occur in Roman mosaic mazes.
Added 11/18/2009 0321654987.10 should also be in this group. I am grateful to Walter D. Pullen for this information.
Added 02/09/2018 0349852167.10 should also be added. Thanks to Andreas Frei!

How are these numbers calculated?

Why did I get interested in this problem?

Where else do these numbers occur?

What else is known about the maze numbers?

References

Return to Main Maze Page

Return to Tony's Home Page

Tony Phillips
Math Dept, SUNY Stony Brook
tony at math.stonybrook.edu
March 17 1997