| Through Mazes |
 |
to Mathematics
|
This page in Polish
Where else do the maze numbers occur?
At the same time (1986-88) that I was investigating the maze numbers
{M(n) = number of different S.A.T. mazes with n levels}
other people in different parts of the world were thinking
about the same mathematical problem.
V. I. Arnol'd
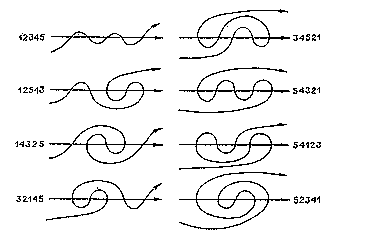 An identical counting problem was proposed by
V. I. Arnol'd in Moscow; it is related to
his work
which appeared in the Siberian Mathematical Journal
of September-October 1988.
Arnol'd
had defined a meander as a connected oriented
non-self-intersecting curve which intersects a fixed oriented
line in several points.
His article contains this figure which, if tilted to the right,
shows exactly the eight maze-paths of
depth 6, and his M5 is the maze number M(6). Arnol'd gives the
first sixteen "meandering numbers," up to
M16 = M(17) = 252939.
An identical counting problem was proposed by
V. I. Arnol'd in Moscow; it is related to
his work
which appeared in the Siberian Mathematical Journal
of September-October 1988.
Arnol'd
had defined a meander as a connected oriented
non-self-intersecting curve which intersects a fixed oriented
line in several points.
His article contains this figure which, if tilted to the right,
shows exactly the eight maze-paths of
depth 6, and his M5 is the maze number M(6). Arnol'd gives the
first sixteen "meandering numbers," up to
M16 = M(17) = 252939.
Vladimir A. Kazakov - Ivan Kostov
At approximately the same time, the calculation of M(n)
came up in another context, this time in the computation of
a matrix integral arising in quantum field theory.
I learned of this work from Alexander Zvonkin, whom I thank
for his correspondence. Later, he and Lando published an
account of this work in their 1993
paper.
Warren Smith
There was another simultaneous and completely
independent occurrence of this problem.
Warren Smith, working on a new, subexponential
traveling salesman algorithm in his 1988 Princeton
thesis
defined jt(N) as the number of topologically distinct ways
in which a Jordan curve can cross an oriented line in the plane at
exactly 2N points, and computed up to jt(10) = M(20) = 8152860.
(May 13 2013) This page has been
translated into Ukrainian by
http://coffeehealtheffects.com.
(June 23 2013) This page has been
translated into
Czech.
Return to Main Maze Page
Return to Tony's Home Page


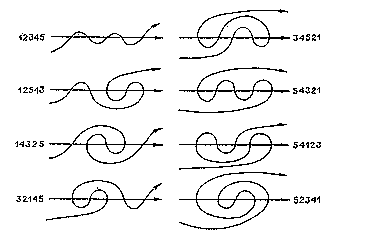 An identical counting problem was proposed by
V. I. Arnol'd in Moscow; it is related to
his work
which appeared in the Siberian Mathematical Journal
of September-October 1988.
Arnol'd
had defined a meander as a connected oriented
non-self-intersecting curve which intersects a fixed oriented
line in several points.
His article contains this figure which, if tilted to the right,
shows exactly the eight maze-paths of
depth 6, and his M5 is the maze number M(6). Arnol'd gives the
first sixteen "meandering numbers," up to
M16 = M(17) = 252939.
An identical counting problem was proposed by
V. I. Arnol'd in Moscow; it is related to
his work
which appeared in the Siberian Mathematical Journal
of September-October 1988.
Arnol'd
had defined a meander as a connected oriented
non-self-intersecting curve which intersects a fixed oriented
line in several points.
His article contains this figure which, if tilted to the right,
shows exactly the eight maze-paths of
depth 6, and his M5 is the maze number M(6). Arnol'd gives the
first sixteen "meandering numbers," up to
M16 = M(17) = 252939.