| Through Mazes |
 |
to Mathematics
|
Unrolling an S. A. T. maze, Duality, Stacking
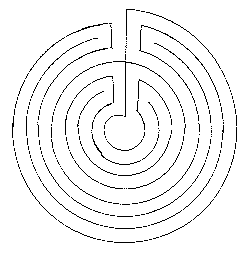
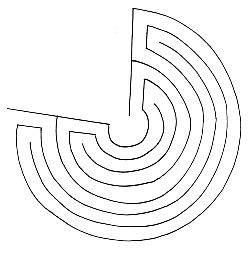
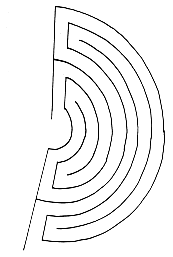
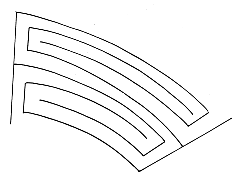
Most simple alternate transit mazes occur in their free state
in a circular form with the path leading from the outside to
the center of the circle. Each such maze can be sliced down its
axis and unrolled into a rectangular form. Now the path enters
at the top of the maze and exits at the bottom: the top level
(center) of
the circular maze becomes the space below the rectangular
form. This process
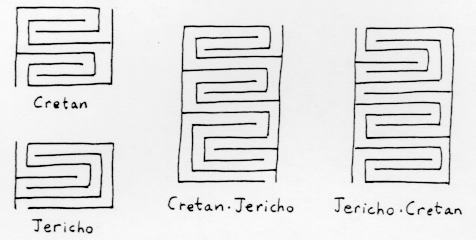
is illustrated here for the Cretan maze.

In rectangular form it becomes clear how each maze has a dual
(read it from bottom to top; the Cretan maze is self-dual)
and how mazes can be composed by
stacking. This operation requires the convention that
all rectangular mazes have their entrance on the same side, say
the right side. Then an even-level maze will exit on the left,
and an odd-level maze will exit on the right. Compose a (2n)-level
maze (top) with
a k-level maze (bottom)
by identifying the (2n)-th level of the top maze with the 0-th
level of the bottom; this gives an s.a.t. maze with 2n+k
levels. Compose a (2n+1)-level
maze (top) with
a k-level maze (bottom) by reversing the bottom maze (so that
its entrance is now on the left) and then identifying the (2n+1)-st
level of the top maze with the 0-th
level of the bottom; this gives an s.a.t. maze with 2n+1+k
levels. Here is how it looks for the 7-level Jericho and
8-level Cretan mazes.
Return to Main Maze Page
Return to Tony's Home Page







