The workshop will follow the SoCG invited talk by Chris Bishop on
Mappings and Meshes
The workshop schedule is
2:20-3:05 Raanan Schul (Stony Brook),
The Traveling Salesman Problem, Data Parameterization and Multi-resolution Analysis
3:05-3:50 Mauro Maggioni (Duke), Multiscale SVD and Geoemtric Multi-Resolution
Analysis for noisy point clouds in high dimensions
3:50-4:10 break
4:10-4:55 Arie Israel (Courant), Interpolation by Sobolev functions
4:55- 5:40 Ken Stephenson (UT Knoxville) Discrete Conformality and
Graph Embedding
5:40-6:10 Open problems and discussion
Classical analysis has always involved geometry in one form or another and in recent years various connections between the techniques of analysis and computational geometry have become more apparent. This workshop will sample a few parts of analysis where the connections are clearest and most important.
Chris Bishop will give a plenary talk at SoCG showing how the
medial axis of planar domains is intimately connected to convex
hulls in 3-dimensional hyperbolic geometry and how this connection plays a role in the
asymptotically fastest known method for computing conformal maps from a
disk to a polygon. Conversely, ideas coming from conformal mapping and
hyperbolic geometry allow one to prove new theorems about triangulations and
quadrilateral meshing of planar domains with optimal angle bounds.
The talk discusses results mostly from
Raanan Schul will speak on the Analyst's Traveling Salesman Problem. Given a set E (possibly infinite), how can we tell if E lies on any finite length curve? In 1991 Peter Jones answered this when E lies in the plane, giving an infinite series associated to the set that converges if and only if the set lies on a rectifiable curve, and the sum of the series giving a bound (up to a constant factor) of the minimal length curve. This series can be thought of as the analog for a set of a wavelet decomposition of a function. Jones theorem was extended to finite dimensional Euclidean spaces by Okikiolu and to infinite dimension space by Schul. There are also versions for more general metric spaces.
Mauro Maggioni will discuss how to efficiently deal with D-dimensional data that lie on a d-dimensional submanfold, with d much smaller than D, and possibly with noise. If the submanifold was a linear space then the standard thing would be to project onto a d-dimensional space using singular values, but for non-linear submanifolds new methods must be used. Maggioni will show how ideas from classical multiscale analysis can be adapted to this setting, introduce the intrinsic dimension of a data set and discuss geometric multiscale analysis for storing and manipulating data sets.
Arie Israel will speak on a topic dating back at least to the work
of Hassler Whitney in the 1930's and 40's: given a function f on a set E in
n-dimensional Euclidean space, can f be extended to the whole space in a nice way,
e.g., as a differentiable function in some sense. If it can be extended, what are
the best bounds on the function and its derivatives that we can deduce from the data?
How fast can we construct an extension that is within a bounded factor of the "best"
extension? Whitney's initial results lay the foundation for much of modern analysis,
but these basic questions lay dormant for many years
until Charles Fefferman and his students (including Israel) recently proved a number of elegant
and surprising results. Israel will describe the progress so far, and how close they
are to complete solutions of these problems.
The talk is based on results in
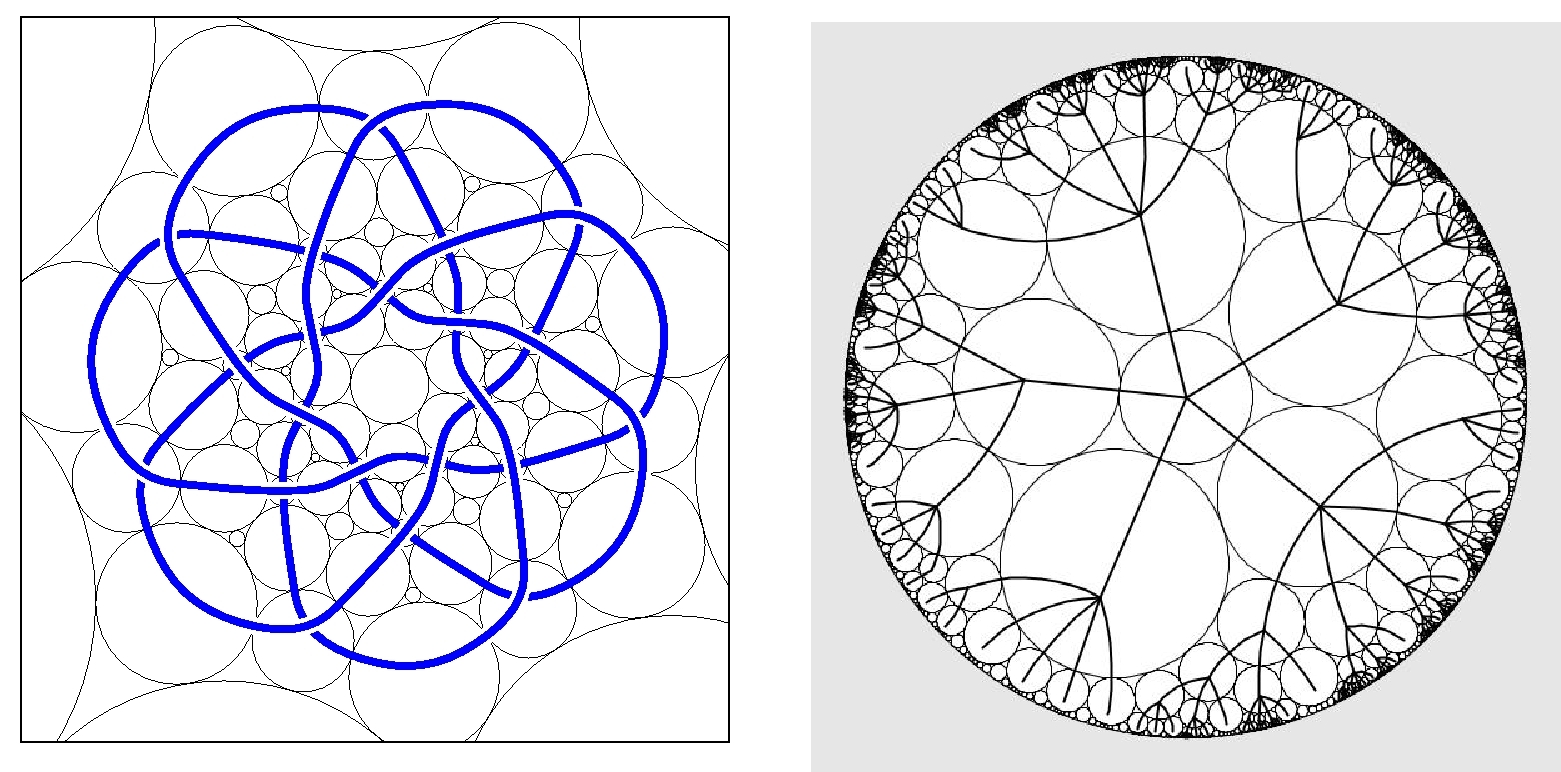
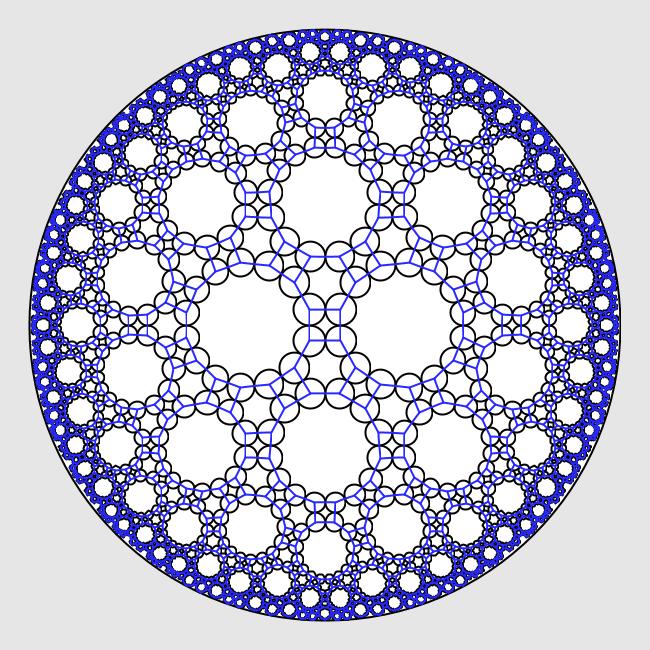
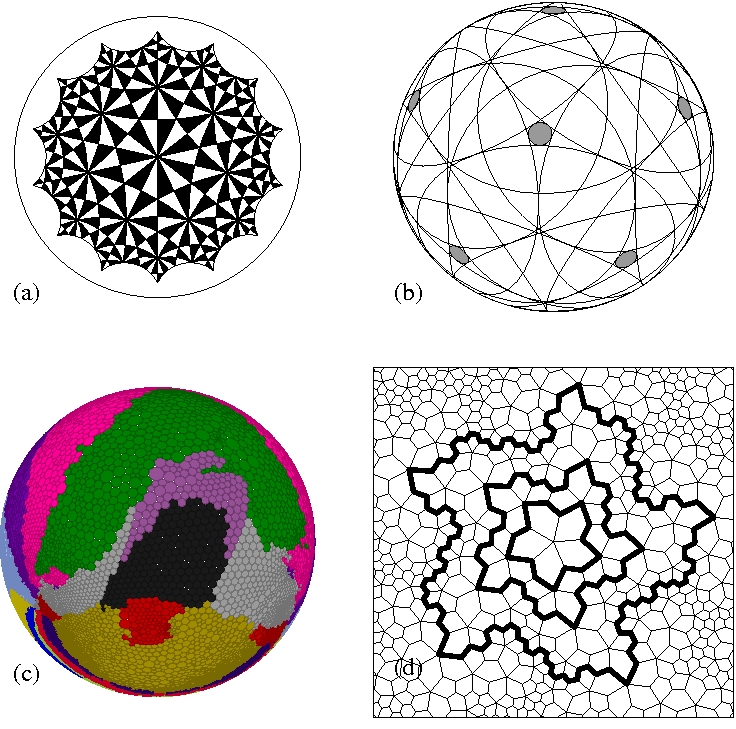
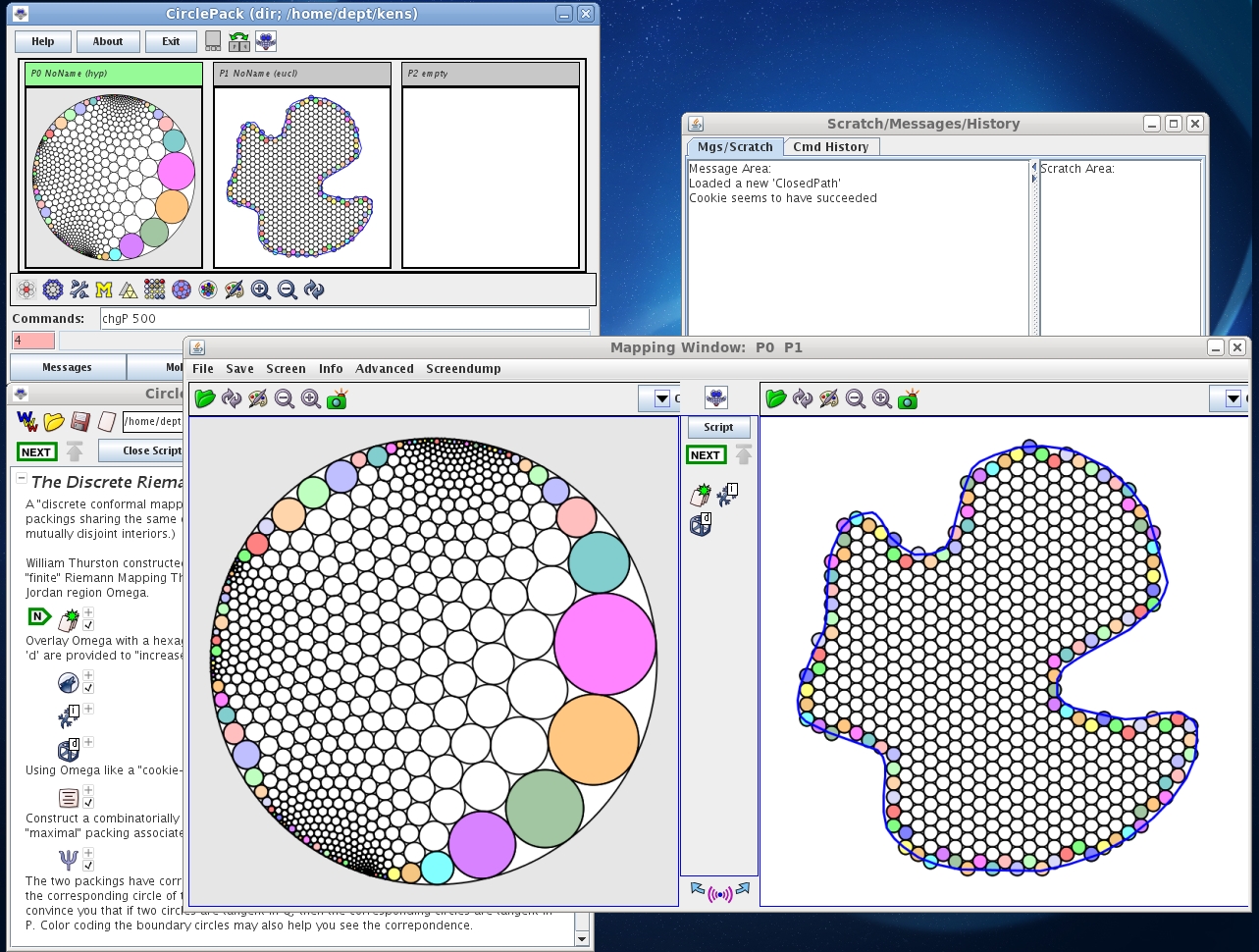
Ken Stephenson literally "wrote the book" on circle packings (his text is the best reference for the area). Whereas classical conformal maps can be thought of as mapping infinitesimal circles to infinitesimal circles, circle packings give rise to a discrete analog of the theory of conformal and holomorphic functions, from which the classical case can be recovered in the limit as the circles shrink (this was conjectured by Thurston and proved by Rodin and Sullivan). In his talk, Stephenson will describe a new application of circle packings to embedding combinatoral graphs into the plane, sphere or disk in a way that is "conformal" in some sense, is easy to compute (even for large graphs) and perserves natural symmetries of the graph. See the figures below.
Some figures by Ken Stephenson (see http://www.math.utk.edu/~kens/ACMChapelHill/):





Some figures by Chris Bishop:
A related workshop on Computational and Conformal Geometry was held April 20-22, 2007 at Stony Brook University. Videos from this conference are available on the Stony Brook Math Department Video Archive.