3. The link to the Golden Mean

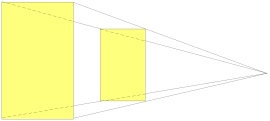
The golden rectangle has the following property: If a square is cut off from one side of the rectangle ...
... the rectangle that remains ...
... has the same ratio of sides as the original rectangle.
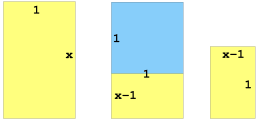
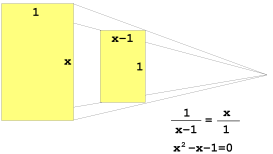
If we call this ratio x, then a rectangle with sides 1 and x will have the correct ratio. The rectangle remaining after cutting away a square will have sides x-1 and 1.
Setting the two ratios equal leads to the equation x2-x-1 = 0.

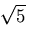We can solve this equation for the Golden Mean: we find one positive root, x= (1+)/2 = 1.618033... This rectangle seems to have nothing to do with a pentagon. Nevertheless,

• In a regular pentagon, the ratio of diagonal to side is the same as the ratio of long side to short in the golden rectangle, namely the Golden Mean 1.618033...(Link to Proof)

• A number is rational if and only if it is commensurable with 1.(Link to Proof).

• 1. What are visual explanations?

• 2. Casselman's visual proof

• 3. The link to the Golden Mean

• 4. Proofs of ancillary facts