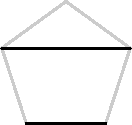
| In this regular pentagon, call the
side length s and the length of the diagonal
d. Our job is to show that s and
d are incommensurable.
First notice that in a regular pentagon,
a diagonal is parallel to the opposite side. This
follows from the symmetry of the pentagon.
|
|
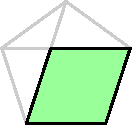
| Using this fact for two adjacent sides
shows that this green quadrilateral is a parallelogram,
with opposite sides equal: all four sides of this
parallelogram have length s.
|
|
| Now suppose that the side and the diagonal
are commensurable: there exists a length h which
fits exactly a whole number of times into the diagonal and
into the side. The length h is symbolized by the
distance between two adjacent dots in this picture.
|

|
The length of the highlighted segment must also
be a whole number of h's, since it is the difference
of two such numbers, d and s. Call this length d*.
d* = d - s.
|

|
The length of this highlighted segment is d - 2d*.
So this length must
also be equal to a whole number of h's. Call this
length s*.
s* = d - 2d* = 2s - d.
|

|
| Now notice that the five diagonals determine
a smaller regular pentagon inside our original one. The side length
of this pentagon is the s* we just considered.
|

|
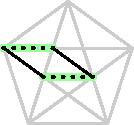
| In the smaller pentagon, the diagonals are again
parallel to the opposite sides. It follows that the highlighted
figure is a parallelogram, and that the diagonal in the smaller
pentagon has length d*.
|
|
| So in the smaller pentagon, side
and diagonal are both multiples of our original h.
|

|
| We can repeat the construction with the
smaller pentagon.
|
 
|
| Since s* is strictly shorter
than s, and they are both whole multiples of h,
they must differ by at least h. We can repeat the
process again and again, and obtain an infinite decreasing sequence
of side lengths s > s* > s** ... each
of which is at least h smaller than the one before.
But this can't work, because there was only a finite number
of h's in s to start! This contradiction shows
that the hypothesis, that s and d are
commensurable, must be false.
|

|
