|
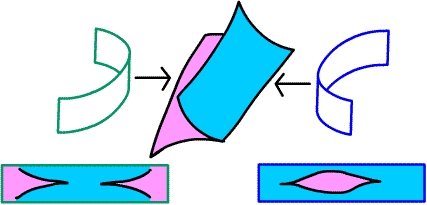
The
beak-to-beak
and
lips
catastrophes are exhibited at the point of tangency of
curved pieces of surface with the cusp locus of the swallowtail.
Embedding them in a one-parameter family (the surface sweeps
across the locus) stabilizes them.
The green-edged piece is concave inward;
at the beginning of the sweep (left to right) it is entirely in the
pink (two-minimum) region. Then its intersection with the pink
region narrows to one central stripe, then two touching beaks, at the point of tangency,
and then two facing
beaks.
The blue-edged piece is
concave outward; during the sweep (right to left)
its intersecton with
the pink
region goes from empty to one point (at tangency)
to the lips configuration.
|