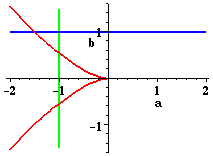
| The (a,b) parameter space for the cusp catastrophe. For parameter values (a,b) in the region between the red curves, the energy function f(x) = x4 + ax2 + bx has two minima. Otherwise it has one. |

The cusp catastrophe is exemplified by the minimum of the function f(x) = x4 at x = 0 . This critical point is unstable: perturbing the function to f(x) = x4 + ax2 gives a function with three critical points (two minima) near zero if a is negative, no matter how small. The minimum of f(x) = x4 has an additional instability: the perturbation f(x) = x4 + ax2 + bx will have two minima near zero if b < (4/3)(-a3/6)1/2 and one otherwise. (For a mechanical instantiation of this catastrophe see The Catastrophe Machine.)

| The (a,b) parameter space for the cusp catastrophe. For parameter values (a,b) in the region between the red curves, the energy function f(x) = x4 + ax2 + bx has two minima. Otherwise it has one. |
| Folllowing from left to right the one-dimensional section given by the blue line, one of the local minima disappears and is captured by the other. The verb class corresponding to this morphology is capture: The fish swallows the bug. |  |
| Following the blue section from right to left, a new local minimum appears beside the old one. The verb class corresponding to this morphology is emission: The bird lays an egg. | 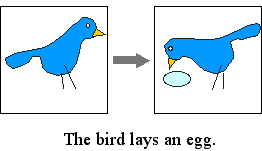 | Following the green line in either direction, one local minimum is substituted by another. The verb class corresponding to this morphology is transformation: The caterpillar becomes a butterfly. | 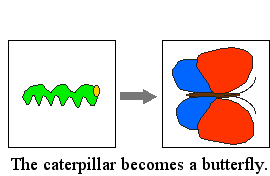
|
corrected 12/14/01.
5. The cusp: "The fish swallows the bug, " etc.
|
|
|
© Copyright 2001, American Mathematical Society |