shell 4

$e-MATH$

The Mathematical Study of Mollusk Shells

4. Things get complicated in three dimensions,

The Molluskville model owed some of its simplicity to being in Flatland; when the same kind of zoning laws are extended to 3-dimensional dwellings the implementation must be more complicated, because the height of the dwelling must be scaled up along with its width and length. This forces each dwelling to approximate an infinite sequence of joined chambers. In that way, when an extra room is added on, the renovation can be similar to the original house.

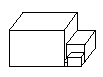
The model house has an infinite sequence of ever-smaller rooms.

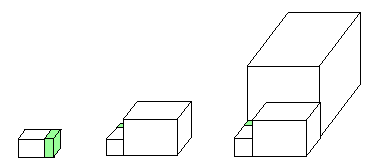
A typical house (the suite of smaller rooms is represented by a single green chamber) and its first three renovations.

but Calculus comes to the Rescue

Since mollusks add onto their shells in small increments (rather than the large rooms in the illusration above) we may approximate the discrete and small by the continuous and the infinitesimal and apply Calculus to determining the mathematical consequence of terminal growth and unchanging form.

We start by supposing that the shell is growing steadily and smoothly as a function of a parameter t, which is a monotonic function of time. If we take a reference point on the growing edge of the shell, it will describe a curve F(t) in 3-space as the organism grows.
Since the shell grows by accretion, the shell at any time T will bear the entire image of the curve up to then. At a later time T+h the image will be the curve F(t+h) for the same t-values. The "unchanging form " requirement means in particular that the new curve must be geometrically similar to the old. Since the seed point, or center, of the shell stays fixed, there must be a 3-dimensional rotation R_h and a dilation D_h which together take the first curve to the second:
F(t+h) = R_h D_h F(t).
Unless F(t)is a straight line, the similarity transformations R_h and D_h are uniquely determined by h and vary smoothly with h. If we compare F(t) with F(t+h₁), F(t+h₂), and F(t+h₁+h₂), we see that the dilation D_{(h₁ + h₂)} must be the composition of the dilations D_h₁ and D_h₂: first you do D_h₁, then you do D_h₂. To dilate a figure you multiply all its dimensions by a "dilation factor." The dilation factor of h₁ + h₂ must therefore be the product of the the dilation factors of h₁ and h₂. Since h=0 must correspond to dilation factor 1, the only possibility is for there to exist a constant v such that D_h is equal to dilation by a factor e^vh.
Similarly the rotation corresponding to h₁ + h₂ must be the composition of the two rotations R_h₁ and R_h₂, for any h₁ and h₂. The R_h therefore form what is called a 1-parameter group of rotations, and there is only one way this can happen: there is a constant c, and a set (x,y,z) of coordinates in 3-space so that, for every h, R_h is the rotation about the z-axis by an angle ch:
R_h(x,y,z) = (x cos(ch) - y sin(ch), x sin(ch) + y cos(ch), z). See For further thought for some more details of this calculation.
Applying the equation F(t+h) = R_h D_h F(t) to h=t and t=0 yields F(t) = R_t D_t F(0), so if F(0) = (x,y,z), in coordinates chosen as above, then the curve F(t) traced out on the shell must be
F(t) = e^vt(x cos(ct) - y sin(ct), x sin(ct) + y cos(ct), z).

This calculation shows how the conditions of terminal growth and unchanging form imply that any reference point on the shell must, during growth, trace out a 3-dimensional equiangular spiral. This matches the D'Arcy Thompson quote at the beginning of this article.

It should be noted that when c=0 the equiangular spiral degerates to the straight line F(t) = e^vt(x,y,z). The corresponding shells, organized as pure cones, do exist, for example in Foraminifers of the genus Dorothia and in the fossil ammonite Didymoceras on exhibit at the American Museum of Natural History.