kepler4

$e-MATH$

Celestial Mechanics on a Graphing Calculator

4. Adaptive Runge-Kutta

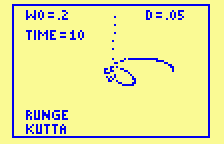
The Runge-Kutta algorithm goes haywire when the curvature of the orbit becomes very large. The remedy is to build into the algorithm a test of how fast the velocity vector is turning; if it would change too much in one step, you decrease the step size (by one half, in this implementation) and try again. Now you do not specify the number of steps, but only a tolerance on how much change in the angle of the velocity vector you will allow in one step. On the other hand, when the velocity vector is not turning much (here, less than one-half the tolerance), you allow the step size to grow (here, by a factor of 2). In this way the algorithm is adapted to the problem.

Comparison of Runge-Kutta and adaptive Runge-Kutta for the same initial conditions. The Runge-Kutta was given 200 steps but ran off the screen before the calculation was completed. The adaptive algorithm did the job in 119 steps, with the step-size controlled to keep the rotation of the velocity vector below .1 radian per step. The program prints out the smallest step size that occurred in the calculation: in this case .002 approximately. To carry out the entire calculation at this step size would have required over 5000 steps.

More eccentric orbits require tighter control on the velocity vector rotation. For w₀=.05 the adaptive Runge-Kutta with rotation tolerance .1 loses control. Taking rotation tolerance .01 does the job.

Comparison of adaptive Runge-Kutta with tolerance .1 radian/step and .01 radian/step. The looser tolerance does not allow a correct approximation of the solution.

With w₀=.05 the orbit is so eccentric that it passes within 1 pixel of the ``sun.'' The program with tolerance .01 takes quite a few minutes to run; but running the whole algorithm at the minimum step size would involve over 2 million steps.