
Celestial Mechanics on a Graphing Calculator
3. The Runge-Kutta algorithm
The Runge-Kutta algorithm (strictly speaking the fourth-order
R-K algorithm; see example) allows
much better accuracy than Euler's method.
Their relative efficiency is like that of Simpson's method
and left-hand sums for approximating integrals, algorithms to
which they are closely related. It was published by
Carle Runge (1856-1927) and Martin Kutta (1867-1944)
in 1901.
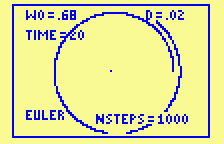
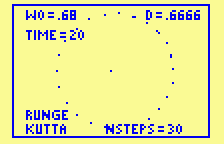
Euler's method and 4th order Runge-Kutta,
applied to the restricted 2-body problem with the same
initial conditions.
The Runge-Kutta method easily accomplishes in 30 steps
what Euler's method could not do in 1000. Even though every
Runge-Kutta step is computationally the equivalent
of 4 Euler steps, the savings are enormous.
But when we decrease w0 to produce
more eccentric elliptical orbits, even this powerful
method starts to strain.
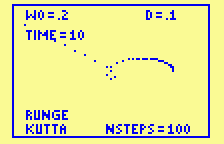
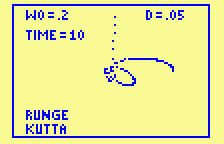
For w0=.2, step
sizes of .1 and .05 lead to non-physical solutions.
Comments: webmaster@ams.org
@ Copyright 2001, American Mathematical Society.






